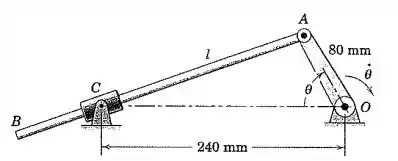
A manivela gira no sentido horário na taxa constante . A haste AB passa através do cursor articulado em C. Determine a velocidade máxima em que AB passa através do cursor e o valor correspondente de Represente graficamente contra para , onde é a distância AC.

Bom pessoal, vamos representar o mecanismo para tirar algumas relações entre suas variáveis:

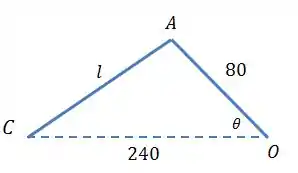
A velocidade da haste AB através do cursor C nada mais é que , que deve estar na direção do cursor. Deste modo, é a derivada de que é a taxa que a haste está aumentando em função do tempo. Então, vamos relacionar com o ângulo através da lei dos cossenos:

Ou

Para encontrar a velocidade , podemos derivar a equação (1):

Para deixar a equação apenas em função de , vamos substituir pelo encontrado na equação (2) e :

Agora vamos plotar o gráfico (em radianos) da expressão acima para o intervalo

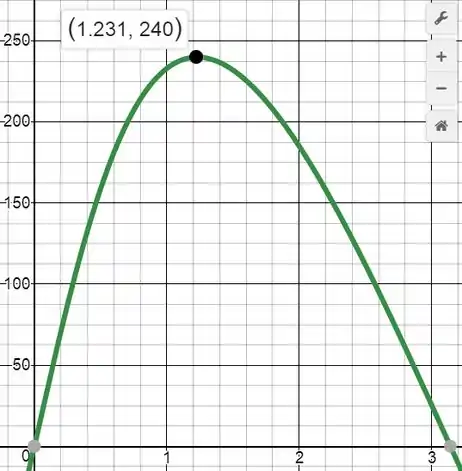
Do gráfico, tiramos que no instante que é máximo: