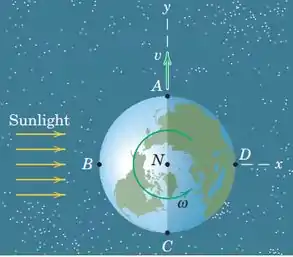
Determine a aceleração do ponto B no equador da Terra, reapresentado aqui a partir do Prob. 5/64. Utilize os dados Fornecidos naquele problema e assuma que a trajetória orbital da Terra é circular, consultando a Tabela D/2 quando for necessário. Considere o Sol fixo e despreze a inclinação do eixo da Terra.
Passo 1
Fala galera! Vamos ter que consultar o exercício 5.64 e a tabela D/2 para buscar os dados necessários para a resolução.
Dados:
Constante Gravitacional:
Massa da Terra:
Massa do Sol relativa a Terra:
Velocidade angular da Terra:
Raio da Terra:
Velocidade da órbita:
Raio da órbita:
Agora com os dados, podemos nos concentrar no que a questão pede.
Para descobrir a aceleração do ponto B, vamos usar o método da aceleração relativa em relação ao centro N. Lembrando a equação:
Onde:
é a aceleração relativa normal e ela aponta para o centro O.
é a aceleração relativa tangencial e ela é perpendicular à distancia AO.
Como a Terra não possui aceleração em sua rotação, então não há aceleração angular , o termo
Outra coisa importante lembrar é a Lei da Gravitação Universal de Newton, em que a aceleração é dada por:
Sendo o Sol a referência.
Passo 2
É muito importante fazermos o esboço com os vetores aceleração neste exercício. Isso para observar a direção e sentido das acelerações.
Veja que há duas acelerações normais!! Calma, calma, não criemos pânico!
Primeiro, temos a aceleração normal do movimento de translação da Terra na órbita com o Sol .
A outra é a aceleração normal do movimento de rotação da Terra em torno de seu próprio eixo . Veja a Figura:
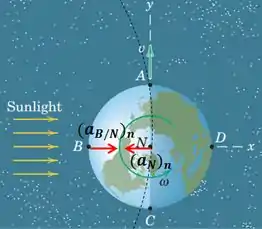
Ahhhh, agora sim!!
Passo 3
Agora é só calcular!
- Aceleração normal do movimento de translação.
-Aceleração normal do movimento de Rotação.
Agora, voltando para a equação geral: