Explica como os valores da massa e da constante de mola k podem ser determinados experimentalmente se a massa é conhecida. Desenvolva expressões para e k em termos dos resultados experimentais especificados. Observe a existência de pelo menos três maneira de resolver o problema.
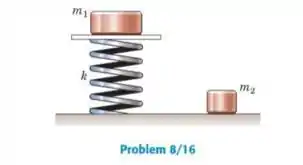
Passo 1
Vamos primeiro colocara massa sobre a mola para observarmos e medirmos a frequência natural:
Passo 2
Depois colocamos a segunda massa junto com a primeira e observamos e medimos as novas frequências:
Passo 3
Por fim, resolvemos o sistema das duas equações para cada uma das incógnitas e k, para isso, podemos fazer a razão entre as duas equações para obtermos :
Isolando :
E então basta substituir na equação de :
Isolando k:
Passo 4
Outras duas maneiras de resolver seriam:
1- Colocar a massa primeiro e observar a frequência, e depois colocar a massa enquanto a massa anterior ainda está na mola, e observar a nova frequência;
2- Colocar a massa e observar a frequência, então retirar a massa e então colocar a massa e observar a frequência.