Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas Fundamentais - Ex. 25
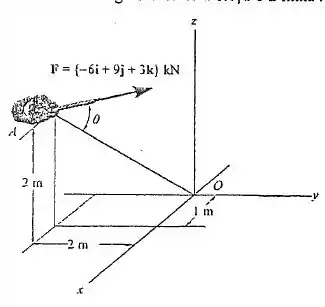
Determine o ângulo entre a força e a linha .
Passo 1
Fala, querido! Queremos o ângulo entre a força e o segmento .
Para determinarmos o nosso ângulo , precisaremos encontrar os vetores que compõem o nosso .
Como assim compõem? Relaxa querido, temos estes vetores aqui:
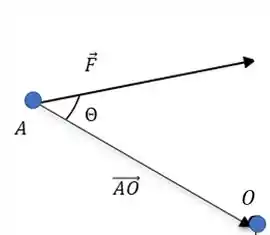
Ou seja, a gente pode achar um vetor na direção de . Aí nosso ângulo está entre dois vetores, e .
E olha que lindo, temos uma fórmula para achar o ângulo entre dois vetores que vem da definição do produto escalar entre eles. Podemos usar essa belezinha aqui:
O que a gente precisa fazer é achar (porque o enunciado já deu ), os módulos dos vetores, o produto escalar entre eles e depois jogar tudo nessa fórmulinha. Vamos lá!
Passo 2
Vamos primeiramente encontrar o vetor . Para isto, temos que encontrar os pontos e .
Para o ponto :
E para o ponto :
Como temos os pontos e , ficou fácil determinar o vetor :
Para determinar um vetor a partir de pontos, basta aplicarmos esta fórmula aqui:
Considerando as coordenadas de como inicial e as coordenadas de como final, temos:
Passo 3
Vamos determinar os módulos dos nossos vetores:
Determinando o módulo do vetor :
Bem o vetor de o enunciado já nos forneceu,
logo, vamos calcular apenas seu módulo.
Passo 4
Vamos agora calcular o produto escalar entre nossos vetores:
Não importa a ordem dos vetores quando a gente faz o produto escalar, tá? Daria o mesmo se fizéssemos .
Calculando
E como a ordem não faz diferença
Passo 5
Agora a gente joga nossos resultados na nossa fórmulinha do passo 1
Aplicado o arco cosseno, nosso ângulo é: