Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas Fundamentais - Ex. 27
Determine o ângulo entre a força e a linha .
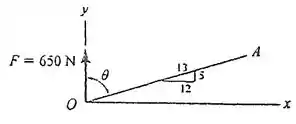
Passo 1
Queremos a relação entre o vetor força e a linha , faremos através dos seus vetores unitários, para isso, vamos encontrar o vetor unitário que determina a direção e o sentido da linha, usaremos a relação de catetos e hipotenusa já que a informação nos é dada através de um triângulo, assim:
Já o vetor unitário de é bem simples já que ela está no eixo :
Passo 2
Podemos então encontrar o ângulo pedido, pela relação:
Sabendo que no produto escalar de dois vetores multiplicam-se suas componentes e correspondentes e somam-se esses produtos:
Resposta
Exercícios de Livros Relacionados
Se a força resultante que atua sobre o suporte é F R = - 300 i + 650 j + 250 kN , determine a intensidade e os ângulos de direção coordenados de F .
O mastro está submetido às três forças mostradas. Determine os ângulos de direção coordenados α 1 , β 1 , γ 1 de F 1 , de modo que a força resultante que atua no mastro seja F R = 350 iN .
A engrenagem está submetida às duas forças caudadas pelo contato com outras engrenagens. Determine a resultante das duas forças e expresse o resultado como um vetor cartesiano.
Se a força resultante que atua sobre o gancho é F R = 200 i + 800 j + 150 k N, determine a intensidade e os ângulos de direção coordenados de F .
Se a força resultante que atua sobre o suporte precisa ser F R = 800 jN , determine a intensidade e os ângulos de direção coordenados de F .