Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas Fundamentais - Ex. 22
Expresse a força como um vetor cartesiano.
Passo 1
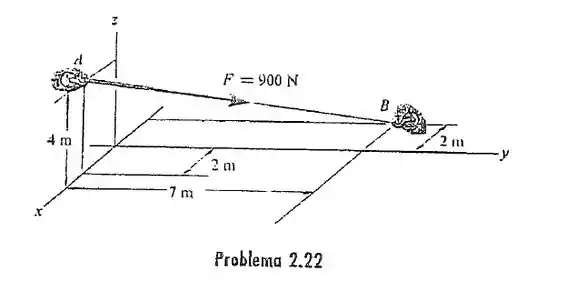
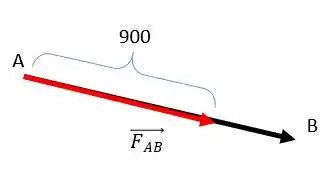
Fala ai galerinha bonita, tudo beleza? Nesse exercício aqui o enunciado nos deu uma força atuando sobre um suporte como na figura abaixo:
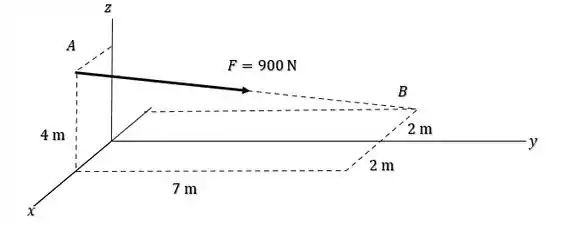
E pediu pra gente encontrar a força na forma de um vetor cartesiano.
Para determinar o vetor em forma cartesiana, existem duas formas, uma delas é por meio de trigonometria e a outra é determinando o vetor unitário da força.
Como assim vetor unitário?
O vetor unitário nada mais é que a um vetor de valor , ou seja, multiplicar o valor de pelo vetor unitário resultará no vetor que desejamos, pois, será o vetor unitário que determinar direção e sentido e por ele ser unitário não estará alterando a real intensidade da nossa força.
Partiu determinar esse tal de vetor unitário então!!
Passo 2
Para determinar o vetor unitário, vamos primeiramente encontrar o vetor .
Para isto, temos que encontrar os pontos e pela figura. Lembrando que os termos são da forma :
Para o ponto :
E para o ponto :
Observe que nesse caso é negativo porque está no sentido negativo do eixo.
Ainda bem que enunciado nos deu esse desenho não é mesmo.
Passo 3
Como temos os pontos e , podemos determinar o vetor , que chamarei de .
Para determinar um vetor a partir de pontos a gente pega o ponto final e subtrai do inicial:
Se a gente for expressar em termos de vamos ter o seguinte:
Observe que:
Substituindo:
Passo 4
Olha que bacana temos nosso vetor , agora determinaremos o nosso vetor unitário. Para fazer é só dividir o vetor pelo seu módulo
Pela seguinte fórmula:
O vetor unitário sera determinado pela divisão do vetor e seu módulo.
Bem, o vetor nos já temos, falta determinar o módulo dele.
Determinando o módulo do vetor :
Passo 5
Temos encontramos o vetor e calculamos o seu módulo, basta e finalmente determinar o vetor unitário :
Perceba que estávamos trabalhando com unidades de metros e ao executar nosso vetor unitário, temos um vetor adimensional.
Passo 6
Temos o vetor unitário, e a intensidade da nossa força. Multiplicando intensidade pelo vetor unitário resultará na nossa força em coordenadas cartesianas .
obs: Caso você desejar verificar se nosso resultando está correto, basta calcular o módulo deste vetor o resultado será sua intensidade de .