Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 147

Determine o centro de gravidade da chapa metálica conformada tal como mostra a figura.

Passo 1

Vamos começar o exercício dividindo o corpo em 4 partes, vamos chamar de parte 1 o triângulo superior, parte 2 a casca esférica, parte 3 o retângulo inferior e parte 4 o recorte semicircular nesse retângulo, então, organizando as informações de interesse em uma tabela, temos:

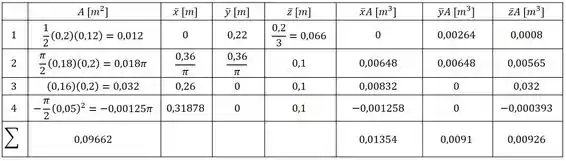
E, nós sabemos que podemos relacionar o centroide com a área superficial pela seguinte equação:

X - ∑ A = ∑ x - A

Então, substituindo os valores encontrados presentes na tabela para x :

X - 0,09662 = 0,01354 → X - = 0,14   m

Passo 2

Fazendo a mesma coisa para y :

Y - ∑ A = ∑ y - A

Então, substituindo os valores encontrados presentes na tabela para y :

Y - 0,09662 = 0,00912 → Y - = 0,094   m

Passo 3

Fazendo a mesma coisa para z :

Z - ∑ A = ∑ z - A

Então, substituindo os valores encontrados presentes na tabela para z :

Y - 0,09662 = 0,00926 → Z - = 0,096   m

Resposta

X - = 0,14   m

Y - = 0,094   m

Z - = 0,096   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra uniforme é encurvada na forma de uma parábola e tem um peso por unidade de comprimento de 100N / m . Determine as reações no apoio fixo A .
Calcule o centroide da área a seguir:
Calcule o centroide da área a seguir:
Calcule o centroide da área a seguir:
Calcule o centroide da área a seguir: