Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 220

Determine as coordenadas xey do centróide da área sombreada. Avalie suas expressões para θ = 0 e θ = 90∘.

Passo 1

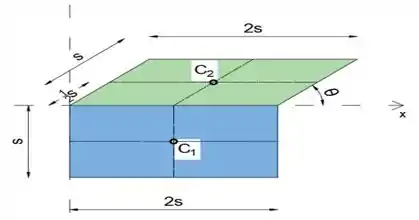
A fim de determinar a coordenada xe y do centróide da área sombreada, vamos dividi-la em duas áreas com todas as dimensões necessárias mostradas no esboço abaixo

Podemos escrever a expressão para a coordenada x do centróide como

x - = x 1 A 1 + x 2 A 2 A 1 + A 2 (1)

y = y 1 A 1 + y 2 A 2 A 1 + A 2 (2)

Passo 2

Coordenada x do centroide da parte 1

x 1 = 2 s 2 = s

Coordenada x da parte 2

x 2 = s + 1 2 s c o s ⁡ θ x 2 = s 1 + 1 2 c o s ⁡ θ

Superfície da área 1

A 1 = s ⋅ 2 s = 2 s 2

Superfície da área 2

A 2 = 2 s ⋅ s s i n ⁡ θ A 2 = 2 s 2 s i n ⁡ θ

Por fim, vamos colocar os valores calculador na equação (1)

x - = s ⋅ 2 s 2 + s 1 + 1 2 c o s ⁡ θ ⋅ 2 s 2 s i n ⁡ θ 2 s 2 + 2 s 2 s i n ⁡ θ

Observe que 2s ³ é incomum para ambas as partes do numerador enquanto 2s² é incomum para ambas as partes do denominador

x - = 2 s 3 1 + 1 + 1 2 c o s ⁡ θ s i n ⁡ θ 2 s 2 ( 1 + s i n ⁡ θ )

Expressão final para a coordenada x do centroide

x - = s 1 + 1 + 1 2 c o s ⁡ θ s i n ⁡ θ 1 + s i n ⁡ θ

Passo 3

Coordenada y do centroide da parte 1

y 1 = - 1 2 s

Coordenada y do centroide da parte 2

y 2 = 1 2 s s i n ⁡ θ

Área da superfície da parte 1

A 1 = s ⋅ 2 s = 2 s 2

Área da superfície da parte 2

A 2 = 2 s - s s i n ⁡ θ A 2 = 2 s 2 s i n ⁡ θ

Passo 4

Por fim, colocaremos os valores na expressão (2)

y - = - 1 2 s ⋅ 2 s 2 + 1 2 s s i n ⁡ θ ⋅ 2 s 2 s i n ⁡ θ 2 s 2 + 2 s 2 s i n ⁡ θ

Observe que s ³ é incomum para ambas as partes do numerador enquanto 2s² é incomum para ambas as partes do denominador

y - = s 3 - 1 + s i n 2 ⁡ θ 2 s 2 ( 1 + s i n ⁡ θ )

Substituiremos s i n 2 ⁡ θ - 1  by  ( s i n ⁡ θ - 1 ) ⋅ ( s i n ⁡ θ + 1 )

y - = s 3 ( s i n ⁡ θ - 1 ) ⋅ ( s i n ⁡ θ + 1 ) 2 s 2 ( 1 + s i n ⁡ θ )

Expressão final da coordenada y do centroide

y - = s 2 ( s i n ⁡ θ - 1 )

Passo 5

p a r a   θ = 0 coordenadas do centroide são

x - θ = 0 = s 1 + 1 + 1 2 c o s ⁡ 0 s i n ⁡ 0 1 + s i n ⁡ 0 x - θ = 0 = s y ̸ θ - 0 = s 2 ( s i n ⁡ 0 - 1 ) y - θ = 0 = - s 2

Para θ = 90 ∘ coordenadas do centroides são

x - θ = 90 ∘ = s 1 + 1 + 1 2 c o s ⁡ 90 ∘ s i n ⁡ 90 ∘ 1 + s i n ⁡ 90 ∘ x - θ = 90 ∘ = s y - 9 - 00 ∘ = s 2 s i n ⁡ 90 ∘ - 1 y θ - 00 ∘ = 0

Resposta

Para   θ = 0

x - = s 1 + 1 + 1 2 c o s ⁡ θ s i n ⁡ θ 1 + s i n ⁡ θ y - = s 2 ( s i n ⁡ θ - 1 )

Para θ = 90 ∘

x - = 8         y - = - s 2 x - = s         y - = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o centroide do sólido obtido pela rotação da área sombreada da figura em torno do eixo x .
Determine por integração direta o centroide da área mostada na figura. Demonstre sua resposta em termos de a e b .
Determine por integração direta o centroide da área a seguir. Determine sua resposta em termos de a e b .
Determine por integração direta o centroide da área a seguir. Determine sua resposta em termos de a e h .
Determine as coordenadas do centroide por integração em termos de a e b :