Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 32

A mola está livre quando θ = 45 º   e tem uma rigidez k = 20   k N / m   . Determine o ângulo θ para o equilíbrio se cada um dos cilindros pesa 250 N. Despreze o peso dos membros.

Passo 1

Desenhando o DCL:

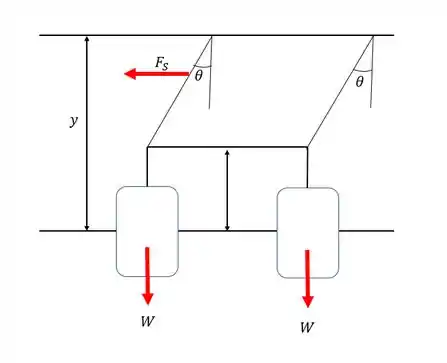
Passo 2

Os pesos estão localizados a uma distância y   acima da referência tomada como base. Os cilindros têm peso W e realizam trabalho positivo ao retornar para posição original.

Tomando y como negativo, a energia potencial gravitacional do peso dos cilindros W é então dada por:

V g =   -   ∑ W y

Sabendo que y = 1,2 c o s θ + b V g = - 2 × 250 × 1,2 c o s θ + V g =   - 600 ⋅ c o s θ - 500 b

Passo 3

Calculando a energia potencial da mola:

V g = 1 2 k s 2

Os elongamentos da mola é dado por:

s = s - s 0 s = 0,6 sen ⁡ 45 º - 0,6 s e n θ s = 0,4242 - 0,6 s e n θ

Calculando a energia potencial:

V e = 1 2 20 × 10 3 0,4242 - 0,6 s e n θ 2 V e = 10 × 10 3 ( 0,18 + 0,36 sen 2 ⁡ θ - 0,5 s e n θ V e = 3600 sen 2 ⁡ θ - 5000 s e n θ + 1800

Passo 4

Calculando a energia potencial do sistema:

V = V g + V e V = - 600 c o s θ - 500 b + 3600 sen 2 ⁡ θ - 5000 s e n θ + 1800

Passo 5

O último passo é achar o ângulo que proporciona o equilíbrio. Calculamos a segunda derivada da expressão da energia potencial e igualamos a zero:

d V d θ = 0 d V d θ = d d θ ( - 600 c o s θ - 500 b + 3600 sen 2 ⁡ θ - 5000 s e n θ + 1800 )

d V d θ = 600 s e n θ + 3600 ⋅ 2 s e n θ c o s θ - 5000 s e n θ d V d θ = 7200 e n θ c o s θ - 5000 s e n θ + 600 s e n θ

Essa equação não tem solução analítica, sendo possível resolver por tentativa e erro. Utilizando um software computacional chegamos ao ângulo:

θ = 38,8 º

Resposta

θ = 38,8 º

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o mecanismo está em equilíbrio quando θ = 30 º º, determine a massa da barra BBC. A mola tem uma rigidez k = 2 kN/m e está livre quando θ = 0 º º. Despreze a massa das ligações
O cilindro é feito de dois materiais de modo que tem uma massa m e um centro de gravidade no ponto G. Mostrre que, quando G se encontra acima do centroide C do cilindro, o equilíbrio é instável.
Determine os ângulos θ para haver equilíbrio do cilindro de 50 kg e investigue a estabilidade em cada posição. A mola está livre quando θ = 60 º º
A xícara tem um fundo hemisférico e uma massa m. Determine a posição h do centro de massa G de modo que a xícara esteja em equilíbrio indiferente.
O caminhão tem uma massa de 200 Mg e um centro de massa G. Determine o grau de inclinação ao longo do qual ele possa estacionar sem tombar e investigue a estabilidade nessa posição.