Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 132
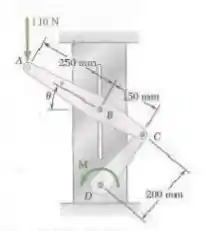
O pino em é fixado ao elemento e pode deslizar livremente ao longo do rasgo aberto na placa fixa. Desconsiderando o efeito do atrito, determine o binário necessário para manter o sistema em equilíbrio quando .
Passo 1
Desejamos encontrar o valor do momento de binário que é necessário para que o sistema em questão esteja em equilíbrio para , ou seja, para esse ângulo devemos ter as forças se anulando. Vamos analisar, primeiramente, o membro cujo diagrama de corpo livre é dado por
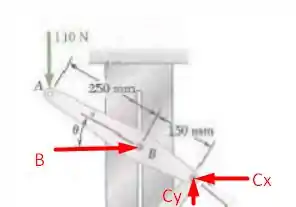
Utilizando as condições de equilíbrio vamos ter
Passo 2
Façamos a mesma análise para o membro e vamos obter o seguinte
Analisando o ângulo destacado em preto teremos
Adotando o sentido anti-horário como positivo vamos ter
Resposta
Exercícios de Livros Relacionados
Para testar a deflexão da viga uniforme de 100 kg, o garoto de 50 kg dá um puxão de 150 N na corda, como mostrado. Calcule a força suportada pelo pino na dobradiçaO.
Um caixote de 54k g está apoiado na porta de 27k g da caçamba de uma picape. Calcule a força trativa T em cada um dos dois cabos de sustentação, um dos quais é mostrado. Os centros de gravidade estão
É desejável que uma pessoa seja capaz de iniciar o fechamento da porta do bagageiro de uma van, desde a posição aberta mostrada, com uma força vertical P de 40N . Como um exercício de projeto, determi
Uma chapa quadrada e uniforme de aço com 360m m de comprimento de aresta e uma massa de 15k g está suspensa no plano horizontal pelos três fios verticais, como mostrado. Calcule a força trativa em cad
Certos elementos de uma máquina para fazer gelo em cubo são mostrados na figura. (Um “cubo” tem a forma de um segmento cilíndrico!) Uma vez que os cubos e um pequeno aquecedor (não mostrado) formam um