Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 88

Determine o valor m e f da massa do sistema (b) de modo que a frequência do sistema (b) seja igual à do sistema (a). Note que as duas molas são idênticas e que a polia do sistema (a) é um cilindro homogêneo maciço de massa m 2 . O cabo não desliza sobre o cilindro.

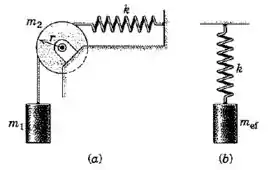
Passo 1

Vamos começar montando uma equação de momentos para o caso (a), em torno do centro O da polia.

∑ M O = I O θ ¨

Vamos montar um esquema que nos ajude a calcular o momento resultante:

∑ M O = T - k x r

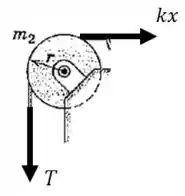
E o momento de inércia da polia em relação ao seu centro é:

I O = 1 2 m 2 r 2

Então:

T - k x r = 1 2 m 2 r 2 θ ¨

T - k x = 1 2 m 2 r θ ¨

Passo 2

E podemos substituir x = r θ , ou x ¨ = r θ ¨ , então:

T - k x = 1 2 m 2 x ¨

T = 1 2 m 2 x ¨ + k x

Além disso, aplicando a segunda lei de Newton sobre a massa m 1 na direção vertical (considerando apenas as forças que contribuem para o movimento oscilatório):

∑ F y = m a y

T = - m 1 x ¨

Então:

- m 1 x ¨ = 1 2 m 2 x ¨ + k x

1 2 m 2 + m 1 x ¨ + k x = 0

Nesse caso, a massa efetiva do sistema é:

m e f ' =   1 2 m 2 + m 1

Passo 3

Agora vamos considerar o caso (b), que é bem mais simples: é um sistema massa-mola clássico:

- k x = m e f x ¨

Obs.: Mais uma vez, perceba que não consideramos a força peso, pois podemos considerar que seu único efeito é deslocar o ponto de equilibrio, em torno do qual a massa passará a oscilar.

m e f x ¨ + k x = 0

Então, para que os dois sistema tenham a mesma massa efetiva, o valor de m e f deve ser:

m e f = m e f '

m e f = 1 2 m 2 + m 1

Resposta

A massa efetiva deve ser m e f = 1 2 m 2 + m 1 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra uniforme de massa m é livremente articulada em torno de um eixo horizontal que atravessa o ponto O . Assuma pequenas oscilações e determine uma expressão para o fator de amortecimento ζ . Para
O mecanismo apresentado oscila no plano vertical em torno do pino O . As molas, ambas de igual rigidez k , estão comprimidas na posição de equilíbrio θ = 0 . Determine uma expressão para o período τ d
Quando o motor tem sua velocidade gradualmente elevada, uma oscilação vibratória muito grande de todo o motor em torno de O - O ocorre a uma velocidade de 360r p m , o que mostra que essa velocidade c
A placa quadrada uniforme está suspensa em um plano horizontal, pelos quatro cabos presos a seus vértices, a partir dos pontos fixos A e B sobre uma linha horizontal a uma distância b acima da placa.