Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 18

Determine a quantidade de movimento angular do eixo do em relação (a) ao ponto A, (b) ao ponto B.

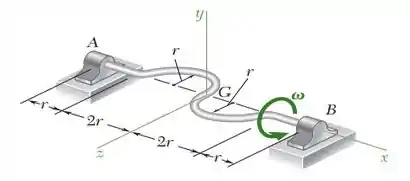
Passo 1

E ai gurizada tudo belezinha??? O enunciado pede que a gente determine a quantidade de movimento angular do eixo do em relação (a) ao ponto A, (b) ao ponto B.

Comprimento da Haste: L = 2   r + 2   π r = 8.2832   r

Velocidade Angular: ω = ω i

Momento angular sobre o ponto G: H G = Ī x ω i - Ī x z ω k

uma vez que o centro de massa G encontra-se no eixo de rotação: v - = 0

Calculo de Ī x e Ī x z :

Passo 2

Deixe ρ = m a s s a por unidade de comprimento = m L

Para a porção AC e DB: I x = 0 ,                         I x z = 0

Para a porção CG use coordenadas polares θ :

x = - r ( 1 - cos ⁡ θ ) ,                     Z = - r sin ⁡ θ ,                       d m = ρ r d θ

I x = ∫ z ²   d m = ∫ 0 π r ² sin ⁡ ² θ     ρ r d θ = π 2   ρ r ³

I x z = ∫ x z     d m = ∫ 0 π r 2 ( 1 - cos ⁡ θ ) sin ⁡ θ     ρ r d θ = 2   ρ r ³

Passo 3

Da mesma forma , para a porção GD:

I x = π 2   ρ r 3 ,                   I x z = 2   ρ r ³

Total: Ī x = π ρ r 3 = π m r ³ L   ,                           Ī x z =   4   ρ r 3 =   4 m r ³ L

H G = π   m r ³ L   ω i - 4   m r 3 L   ω k = m r 2 ω ( 0.37927 i - 0.4829   l k )

Passo 4

(a)Momento angular sobre o ponto A:

H A = H G + r G / A × ( m v - )

H A = H G + 0

Passo 5

(b)Momento angular sobre o ponto B:

H B = H G + r G / B × ( m v - )

H B = H G + 0

Resposta

a) H A = m r 2 ω ( 0.379 i - 0.483 k )

b) H B = m r 2 ω ( 0.379 i - 0.483 k )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cilindro maciço homogêneo é liberado a partir do repouso sobre a rampa. Se θ = 40 ° , μ s = 0,30 e μ k = 0,20 , determine a aceleração do centro de massa G e a força de atrito exercida pela rampa so
A barra uniforme de massa m e comprimento L está deslocando horizontalmente com uma velocidade v sobre seus roletes leves na extremidade. Determine a força sob o rolete B logo após ele passar pelo pon
Determine a aceleração angular de cada uma das duas rodas, enquanto rolam sem deslizar para baixo nos planos inclinados. Para a roda A , examine o caso em que a massa do aro e dos raios é desprezível
A nave espacial está girando com uma velocidade angular constante ω em torno do eixo z , ao mesmo tempo em que seu centro de massa O está se deslocando com uma velocidade v 0 na direção y . Se um jato
A placa de aço quadrada uniforme tem uma massa de 6k g e está em repouso sobre uma superfície horizontal lisa no plano x - y . Se uma força horizontal P = 120N é aplicada na direção e sentido mostrado