Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 94
A polia cilíndriva, maciça e homogênea possui uma massa e um raio . Se a peça em é submetida ao deslocamento harmônico indicado, determine a equação de movimento do sistema em termos da variável . O cabo que liga a massa à mola superior não desliza sobre a polia.
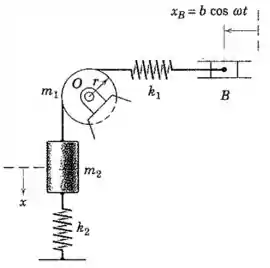
Passo 1
Vamos começar olhando para o momento resultante que age na polia, em relação ao seu centro em :
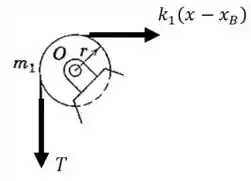
E o momento de inércia da polia em relação ao seu centro é:
Então:
E também podemos aplicar a segunda lei de Newton sobre a massa na vertical:
E o sinal negativo aparece porque ambas as forças favorecem o retorno ao ponto de equilíbrio quando aumenta. (Obs.: pelo desenho, aumenta quando a massa desce).
Passo 2
Então ficamos com duas equações:
Vamos somar as duas para eliminar :
E podemos substituir , e consequentemente :
Então:
Mas segundo o desenho do enunciado , então:
E essa é a equação que foi pedida.
Resposta
A equação do movimento é .