Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 86
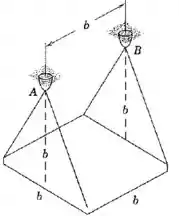
A placa quadrada uniforme está suspensa em um plano horizontal, pelos quatro cabos presos a seus vértices, a partir dos pontos fixos e sobre uma linha horizontal a uma distância acima da placa. Determine uma expressão para a frequência das pequenas oscilações da placa em torno do eixo -.
Passo 1
Vamos começar calculando o momento de inércia em relação ao eixo . Para isso vamos precisar do teorema dos eixos paralelos:
Onde é a distância entre o eixo que passa pelo centro de massa (na direção paralela a ) e o eixo :
Então:
Passo 2
Agora vamos montar uma equação de momentos em torno desse eixo:
E a única força que produz momento em torno desse eixo é o peso:
Então:
E vamos aproximar :
O termo que multiplica é o quadrado da frequência angular, então:
E podemos calcular a frequência da seguinte forma:
Resposta
A frequência de pequenas oscilações é .