Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 11

Um motor transmite um torque M = 0,05 N.m para o centro da engrenagem A. Determine a velocidade angular de cada uma das três engrenagens menores (iguais) em 2 s partindo do repouso. As engrenagens menores (B) estão presas com pinos nos seus centros, e as massas e raios de giração centroidais das engrenagens são dados na figura.

Passo 1

Começaremos o exercício aplicando o princípio do impulso e da quantidade de movimento para a engrenagem A com o auxílio da figura a seguir:

↻ +   H A 1 + ∑ ∫ M A d t = H A 2

0 - 3 F 2 0,04 + 0,05 2 = 0,8 0,031 2 ω A

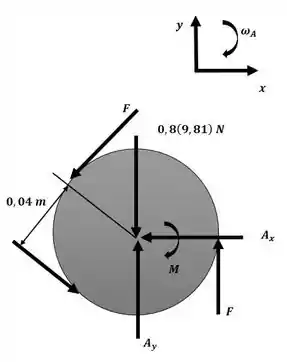
Essa será nossa equação 1. Agora aplicaremos o mesmo princípio, só que para a engrenagem B com o auxílio do diagrama a seguir:

↻ +   H B 1 + ∑ ∫ M B d t = H B 2

0 + F 2 0,02 = 0,3 0,015 2 ω B

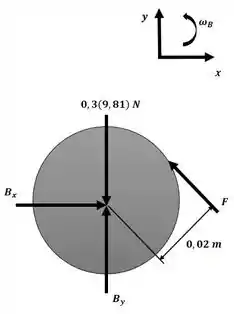
Essa será nossa equação número 2.

Passo 2

Podemos relacionar as velocidades angulares das engrenagens através de seus raios conforme segue:

r A ω A = r B ω B → 0,04 ω A = 0,02 ω B

ω B = 2 ω A

Essa será nossa equação número 3.

Passo 3

Agora podemos substituir a equação 3 na equação 2:

0 + F 2 0,02 = 0,3 0,015 2 ω B

0 + F 2 0,02 = 0,3 0,015 2 ( 2 ω A )

F = 0,003375 ω A

Agora, substituiremos esse valor na equação 1:

0 - 3 F 2 0,04 + 0,05 2 = 0,8 0,031 2 ω A

0 - 3 0,003375 ω A 2 0,04 + 0,05 2 = 0,8 0,031 2 ω A

ω A = 63,3   r a d / s

Por fim, substituindo esse valor na relação de transmissão entre A e B:

ω B = 2 ω A = 2 ( 63,3 )

ω B = 126,7   r a d / s

Resposta

ω B = 126,7   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O fenômeno de “tropeço” de um veículo é investigado aqui. O veículo utilitário esportivo está deslizando para o lado com velocidade v 1 e sem velocidade angular quando atinge um pequeno meio-fio. Assu
Dois pequenos jatos de empuxo variável são acionados para manter a velocidade angular da nave espacial em relação ao eixo z constante em ω o = 1,25r a d / s , enquanto as duas hastes telescópicas são
O disco circular ranhurado de 3,6k g tem um raio de giração em relação ao seu centro O de 150m m e inicialmente está girando livremente em torno de um eixo vertical fixo através de O com uma velocidad
O projeto preliminar de uma unidade para reduzir automaticamente a velocidade de um conjunto que gira livremente é apresentado. Inicialmente a unidade está girando livremente em torno de um eixo verti
Determine a velocidade mínima v que a roda deve possuir para conseguir rolar por cima da obstrução. O raio de giração centroidal da roda é k , e se supõe que a roda não deslize.