Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 23

O disco circular de 25 kg está fixado ao garfo através de um eixo liso A. O parafuso C é usado para travar o disco ao garfo. Se o garfo é submetido a um torque M = 5 t 2   N . m , onde t é dado em segundos e o disco é destravado, determine a velocidade angular do garfo quando t = 3 s, partindo do repouso. Despreze a massa do garfo.

Passo 1

Primeiramente devemos analisar o conjunto. Como o disco não está fixado ao garfo, ou seja, eles não rotacionam juntos, dessa forma, somente o momento linear do centro de massa contribui para o momento angular em torno do ponto O. Sendo assim, o garfo rotaciona em torno do eixo fixo. A imagem a seguir representa o sistema em estudo:

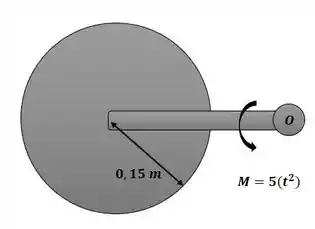
Passo 2

Dessa forma, sabemos que a velocidade em A pode ser escrita como:

v A = ω r O A = ω ( 0,3 )

Passo 3

Agora podemos aplicar o princípio do mento angular em torno do ponto O:

↺ +   H O 1 + ∑ ∫ t 1 t 2 M O d t = H O 2

0 + ∫ 0 3 s 5 t 2 d t = 25 ω 0,3 0,3

5 t 3 3 0 3 s = 2,25 ω

ω = 20   r a d / s

Resposta

ω = 20   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bala de 20 g, disparada contra um bloco de madeira de 4 kg suspenso pelas cordasACeBD, penetra no bloco no pontoE, a meio caminho entreCeD, sem atingir a cordaBD. Determine (a) a altura máximahaté
A bolaBé suspensa por uma corda inextensível. Uma bolaAidêntica é liberada do repouso quando está justamente tocando a corda e cai de uma distância verticalhA= 200 mm antes de bater na bolaB. Consider
Uma esferaAde 700 g, movendo-se com velocidadev0paralela ao chão, atinge a face inclinada de uma cunhaBde 2,1 kg, inicialmente em repouso, que pode rolar livremente sobre o chão. Após o impacto, é obs
Os três blocos mostrados na figura são idênticos. Os blocosBeCestão em repouso quando o blocoBé atingido pelo blocoA, que se move com uma velocidadevAde 3 m/s. Após o impacto, considerado perfeitament
Quando a corda está a um ângulo de α=30 ° a esferaAde 1 kg tem uma velocidadev0= 0,6 m/s. O coeficiente de restituição entreAe cunhaBde 2 kg é 0,8 e o comprimento da cordal= 1 m. A constante da mola t