Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 72
Inicialmente, a roda A gira no sentido horário com uma velocidade anular constante de = 100 rad/s. Se A é colocada em contato com B, que é mantida fixa, determine o número de revoluções antes que a roda A seja parada. O coeficiente de atrito cinético entre as duas rodas é = 0,3 e os raios de giração de A e de B em relação aos seus centros de massa respectivos são = 0,3 m e = 0,225 m. Despreze o peso do membro AC.
Passo 1
Para resolver esse exercício, iremos considerar a aceleração da gravidade como .
Como a roda B é mantida fixa, quando a roda A for colocada em contato com B, haverá força de atrito cinético entre elas, sendo:
Podemos já calcuar o momento de inércia das duas rodas. Para a roda A:
Para a roda B:
Passo 2
No passo 2 iremos aplicar as equações de movimento para a roda A. Para isso, tomaremos como base o seguinte diagrama para a roda A:
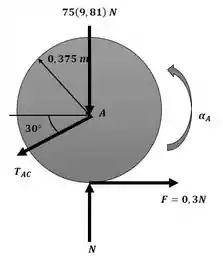
Somatório de momento em torno de A:
Essa será nossa equação número 1.
Somatório de forças na direção x:
Essa será nossa equação número 2.
Somatório de forças na direção y:
Essa será nossa equação número 3.
Isolando N da equação número 2 e substituindo na equação número 3:
Substituindo esse valor na equação 2:
E, para descobrir a aceleração, usaremos esse valor na equação número 1:
Passo 3
Agora iremos aplicar a equação de Torricelli para deslocamento angular e descobrir o número de revoluções necessários para parada:
Por fim, devemos converter o deslocamento de radianos para revoluções, sabendo que uma revolução equivale a 2 radianos: