Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 80

A mangueira está enrolada em uma espiral no carretel e é puxada para fora por uma força horizontal de P = 200 N. Determine a aceleração angular do carretel após ele ter realizado 2 revoluções. Inicialmente, o raio é r = 500 mm. A mangueira tem 15 m de comprimento e tem uma massa por unidade de comprimento de 10 kg/m. Trate a mangueira enrolada como um disco.

Passo 1

Nesse exercício, precisamos levar em consideração que a massa da mangueira enrolada diminui conforme o carretel gira, sabemos que o comprimento de um arco de circunferência é dado pelo produto do raio pelo ângulo, logo, a massa da mangueira enrolada é dada por:

m = l t o t a l m c o m p - r θ ( m c o m p )

m = 15 10 - r θ 10

m = 150 - 10 r θ

Dessa forma, o momento de inércia com relação ao centro de massa é dado por:

I G = 1 2 m r 2 = 1 2 ( 150 - 10 r θ ) ( r 2 )  

Sabemos também que só temos a componente tangencial da aceleração, logo

a = α r

a = 0,5 α

Passo 2

Agora, com o auxílio do diagrama a seguir, podemos aplicar a equação do momento em torno do ponto O:

↺ + ∑ M O = ∑ M k O

- 200 r = - 1 2 150 - 10 r θ r 2 α - 10 r θ α r r

α = 200 75 r + 5 r 2 θ

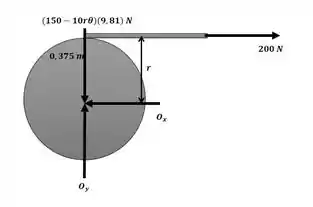
Passo 3

Agora, sabendo que o raio da mangueira enrolada é dada por:

r = 0,5 - θ 2 π w = 0,5 - θ 2 π ( 0,01 )

Conforme pedido no enunciado, queremos analisar a aceleração angular para θ = 2 revoluções, sendo assim, sabendo que isso equivale a 4 π radianos:

r = 0,5 - 4 π 2 π 0,01 → r = 0,48   m

Por fim, usando esse valor na equação para α obtida no passo 2:

α = 200 75 r + 5 r 2 θ

α = 200 75 r + 5 0,48 2 4 π

α = 3,96   r a d / s 2

Resposta

α = 3,96   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

107. O pião de 12g de raio de giração em relação ao seu eixo de giro de 16m m está girando à taxa p = 3600r p m no sentido indicado, com seu eixo de giro fazendo um ângulo θ = 20 ° com a vertical. A d
121. A barra retangular está girando no espaço em torno de seu eixo longitudinal à taxa p = 200r p m . Se seu eixo oscila através de um ângulo total de 20 ° conforme mostrado, calcule o período τ da o
119. Um menino lança um disco circular fino (como um F r i s b e e ) com uma velocidade de giro de 300r p m . Observa-se o plano do disco oscilar através de um ângulo total de 10 ° . Calcule o período
118. Os dois discos circulares idênticos, cada um de massa m e raio r , estão girando com uma unidade rígida em torno de seu eixo comum. Determine o valor de b para o qual não ocorrerá movimento de pr
120. A figura mostra uma bola de futebol americano em três configurações comuns durante o vôo. O caso (a) é um passe em espiral arremessado perfeitamente com uma velocidade de giro de 120r p m . O cas