Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 88

O disco D gira com uma velocidade angular constante no sentido horário de 30 rad/s. O disco E tem uma massa de 30 kg e está inicialmente em repouso quando ele é colocado em contato com D. Determine o tempo necessário para o disco E alcançar a mesma velocidade angular que o disco D. O coeficiente de atrito cinético entre os dois discos é μ k = 0,3 . Despreze o peso da barra BC.

Passo 1

Iremos considerar a aceleração da gravidade g = 9,81   m / s 2 .

Começaremos o exercício calculando o momento de inércia do disco E com relação ao ponto B:

I B = 1 2 m r 2 = 1 2 30 0,3 2

I B = 1,35   k g . m 2

Passo 2

Agora iremos aplicar as equações do movimento para o disco E com o auxílio do diagrama a seguir:

+ →   ∑ F x = m a G x

0,3 N - F B C c o s 45 ° = 0 → F B C = 0,424 N

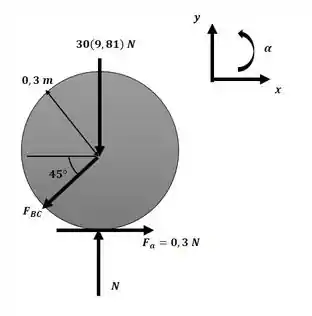
Essa será nossa equação número 1. Agora na direção y temos:

+ ↑   ∑ F y = m a G y

N - F B C s e n 45 ° - 30 9,81 = 0

Essa será nossa equação número 2. Agora o somatório de momentos com relação ao ponto B:

↺ +   ∑ M B = ∑ I B α

0,3 N 0,3 = 1,35 α

Essa será nossa equação número 3.

Passo 3

Agora iremos resolver o sistema de equações encontrado no passo 2. Começaremos substituindo a equação 1 na 2:

N - F B C s e n 45 ° - 30 9,81 = 0

N - ( 0,424 N ) s e n 45 ° - 30 9,81 = 0

N = 420,43   N

Agora iremos substituir esse valor na equação 3:

0,3 ( 420,43 ) 0,3 = 1,35 α

α = 28,03   r a d / s 2

Agora podemos aplicar a equação da cinemática para descobrir o tempo de interesse:

↺ +   ω = ω 0 + α t

30 = 0 + 28,03 t

t = 1,07   s

Resposta

t = 1,07   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada perna de 200 mm das barras de ângulo reto que estão soldados à hastte vertical possui uma massa de 0.12 kg. Calcule o momento fletor M na haste em O devido à rotação do conjunto em torno da haste
Coloque o seu livro sobre sua mesa, com eixos fixos orientados como indicado. Gire o livro em torno do eixo x através de um ângulo 90º e, em seguida, a partir dessa nova posição gire-o 90º em torno do
O robô do Prob. 7/17 é apresentado novamente aqui, onde o sistema de coordenadas x - y - z com origem em O 2 gira em torno do eixo X na velocidade angular θ ˙ . Os eixos sem rotação X - Y - Z orientad
109. Cada uma das rodas idênticas tem uma massa de 4 k g e um raio de giração k z = 120 m m e está montada a uma haste horizontal A B presa à haste vertical em O . No caso (a), a a haste horizontal es
95. O avião a jato na parte inferior de uma acrobacia aérea na forma de um círculo em um plano vertical, tem uma tendência, devido a ação giroscópica do rotor do motor, a mudar de direção para a direi