Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 46
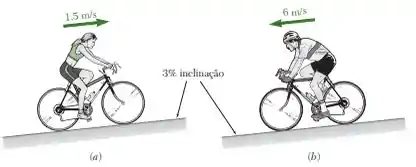
(a) Uma mulher de 60 kg pedala uma bicicleta de 8 kg subindo uma ladeira com 3% de inclinação, a uma velocidade constante de 1,5 m/s. Quanta potência precisa ser desenvolvida pela mulher? (b) Um homem de 90 kg em uma bicicleta de 9 kg começa a descer a mesma ladeira, mantendo com os freios uma velocidade constante de 6 m/s. Qual é a potência dissipada pelos freios? Ignore as resistências do ar e rolamento.
Passo 1
Vamos lá! Esta questão pede para calcularmos a potência em dois casos distintos: uma subida e uma descida em uma ladeira.
Apesar de serem casos distintos, o procedimento aqui será o mesmo! Primeiro, lembramos que a potência é a taxa de variação do trabalho de uma força. Além disto, a potência pode ser calculada por:
Sendo a força atuante, que neste caso é o peso da pessoa e da bicicleta. O cuidado que temos que ter aqui é que a fração do peso que multiplicamos pela velocidade está na direção da velocidade!
Para nos auxiliar nesta decomposição, para uma inclinação da pista (que iremos calcular ainda), temos a seguinte geometria.
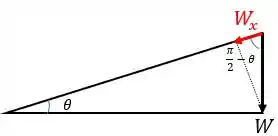
Portanto, a fração de peso é:
Passo 2
Antes de calcularmos a potência, precisamos determinar o ângulo da inclinação. Quando a questão nos diz que a rampa possui uma inclinação de 3%, ela quer nos dizer que:
Portanto, o ângulo é . Agora já podemos calcular as potências! Para a letra a), a potência necessária para a subida da mulher será:
Já para a letra b), a potência será:
E assim finalizamos a questão!