Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.3 - Ex. 61

61. O movimento do carrinho externo B é dado por x B = b ⋅ s e n ω t . Para qual faixa da frequência d excitação ω , a amplitude do movimento da massa m em relação ao carrinho é inferior a 2 b ?

Passo 1

Bom, primeiro, a gente vai designar x m como sendo o deslocamento absoluto do carrinho. Então:

x m = x B + x

Onde x é o deslocamento relativo da massa m dado por ( x = x m - x B ) :

Passo 2

Agora, vamos fazer o diagrama de corpo livre da massa m

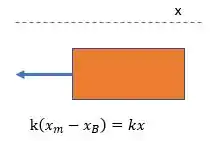
E fazer o somatório de forças em x :

∑ F x = m a x

- k x m - x B = m ( x B ¨ + x ¨ )

- k x = m x B ¨ + m x ¨

Dividindo tudo por m e isolando x B ¨ encontramos que:

- x B ¨ = k m x + x ¨

Mas se lembrarmos que x B ¨ = - b ⋅ ω 2 ⋅ s e n ( ω t ) , obtemos então que:

b ⋅ ω 2 ⋅ s e n ω t = k m x + x ¨

Passo 3

Na equação encontrada, se assumirmos x = X ⋅ s e n ( ω t ) , obteremos:

X = b ω / ω n 2 1 - ω / ω n 2

Para o requisito de X < 2 b

- 2 b < b ω / ω n 2 1 - ω / ω n 2 < 2 b

Então faremos duas desigualdades:

A primeira:

b ω / ω n 2 1 - ω / ω n 2 < 2 b

ω / ω n 2 1 - ω / ω n 2 < 2 → ω / ω n 2 ω n 2 - ω 2 ω n 2 < 2

ω 2 ω n 2 - ω 2 < 2 → ω 2 < 2 ( ω n 2 - ω 2 )

ω 2 < 2 ω n 2 - 2 ω 2 → 3 ω 2 < 2 ω n 2

ω ω n 2 < 2 3

ω ω n < 2 3

A segunda:

b ω / ω n 2 1 - ω / ω n 2 > - 2 b

ω / ω n 2 1 - ω / ω n 2 > - 2 → ω ω n 2 ω n 2 - ω 2 ω n 2 > - 2

ω 2 ω n 2 - ω 2 > - 2 → ω 2 > - 2 ( ω n 2 - ω 2 )

ω 2 > - 2 ω n 2 + 2 ω 2 → - ω 2 > - 2 ω n 2

ω ω n 2 > 2

ω ω n > 2

Resposta

O intervalo para que a amplitude da massa m seja inferior a 2 b é:

ω ω n < 2 3   o u   ω ω n > 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A casca cilíndrive com paredes finas de raio r e altura h é soldada ao pequeno eixo em sua extremidade superior conforme indicado. Determine a frequência circular natural ω n para pequenas oscilações
Uma placa retangular uniforme é articulada em torno de um eixo horizontal que atravessa um de seus vértices conforme mostrado. Determine a frequência natural ω n para pequenas oscilações.
Desenvolva a equação diferencial para pequenas oscilações do pêndulo sob a ação das molas e determine o período τ . A posição de equilíbrio é vertical como indicada. A massa da haste é desprezível.
Determine a frequência natural f n para pequenas oscilações no plano vertical em torno do mancal O para o disco semicircular de raio r .
A placa quadrada fina está suspensa por uma cavidade (não mostrada) que se encaixa na pequena esfera de fixação em O . Se a placa é levada a oscilar em torno do eixo A - A , determine o período para p