Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 133
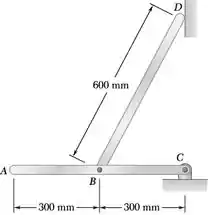
Duas barras uniformes de 4 kg estão ligadas formando o sistema articulado mostrado na figura. Desprezando o efeito do atrito, determine a reação em D imediatamente após o sistema articulado ser liberado do repouso na posição mostrada na figura.
Passo 1
Barra AC:
Rotação sobre C
Passo 2
Barra BC:
Deve ser zero desde
Cinética:
Barra BD
Passo 3
Barra AC:
Substitua da Eq. (1) para By
Eq. (2),
Resposta
Exercícios de Livros Relacionados
O cilindro de 12 kg sustentado pelos suportes dos mancais em A e B tem um momento de inércia em relação ao eixo vertical z 0 por meio de seu centro de massa G igual a 0,080k g ∙ m 2 . O disco e os sup
Cada uma das duas barras esbeltas uniformes O A e B C possui uma massa de 8k g . As barras estão soldadas em A para formar um elemento com formato de T e estão girando livremente em torno de um eixo h
A haste B de 0,4k g com centro de massa a 55m m de O - O tem um raio de giração de 69m m em relação a O - O . A haste está soldada ao tubo de aço e é livre para girar em torno do eixo horizontal fixo
Um cabo flexível com 60 metros de comprimento, com uma massa de 0,160k g por metro de comprimento, está enrolado em volta do tambor. Com y = 0 , o peso do cilindro de 4k g é necessário para iniciar a
Em 1993 , o ônibus espacial capturou o telescópio Hubble em órbita e fixou-o ao compartimento de carga para reparos, na configuração simulada na figura. Durante o período de reparo era importante limi