O embolo de 5 kg acionado O bloco quadrado homogêneo de massa é liberado a partir do repouso com quase nulo e gira no ponto médio de sua base em torno da quina fixa em . Determine e represente graficamente as forças normal e tangencial, expressas nas formas adimensionais e , exercidas sobre o bloco pela quina como funções de (a). Se um pequeno entalhe em impede o bloco de deslizar, determine o ângulo em que o contato com a quina cessa. (b) Na ausência de um entalhe e com um coeficiente de atrito estático de , determine o ângulo em que o deslizamento inicia.

Passo 1
Primeiramente é necessário determinar o DCL do corpo em analise, confomer a figura abaixo mostra.

Também é necessário determinar o momento de inercia do bloco para somatório de momentos
Passo 2
Realizando o somatório de momentos em relação afim de eliminar :
Além dos somatório de forçao e momentos será necessário uma quarta equação, que é obtida utilizando -se a cinemática, onde podem ser relacionados a pela equação:
Para os somatório de forças
Passo 3
- Para as equações,
- Considerando a ausência de um entalhe e com um coeficiente de atrito estático de
E,
Gráfico do comportamento das mesma é
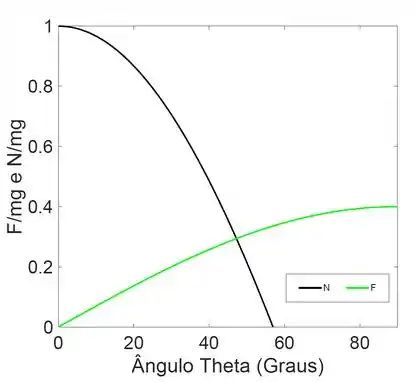
Quando a força normal é zero.
A força de atrito
E utilizando uma analise adimensional temos que,
Utilizando o método de Newton para determinar
Resposta
As expressões para e são e . Quando a força normal é zero. E o ângulo em que o deslizamento inicia é