Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 87
O tambor tem uma massa de 25 kg e um raio de giração . Uma corrente de 10,5 m de comprimento tendo uma massa de 3 kg/m está enrolada em torno da superfície exterior do tambor, de maneira que um comprimento de corrente de s = 0,9 m está suspenso, como mostrado. Se o tambor está originalmente em repouso, determine sua velocidade angular após a extremidade B descer s = 3,9 m. Despreze a espessura da corrente.
Passo 1
Iremos considerar a aceleração da gravidade .
Começaremos o exercício aplicando o somatório de momentos com relação ao ponto A com o auxílio do diagrama a seguir:
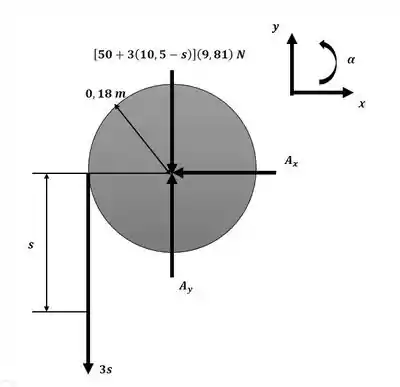
Passo 2
Agora iremos usar a seguinte relação apresentada no livro:
Resposta
Exercícios de Livros Relacionados
110. Se a roda no caso (a) do problema 7 / 109 é forçada a executar uma precessão em torno da vertical, por um acionamento mecânico na taxa constante de Ω = 2 j ^r a d / s , determine o momento fletor
A empilhadeira manual tem uma massa de 70 kg e centro de massa em G. Determine a maior aceleração para cima da bobina de 120 kg de maneira que nenhuma reação sobre as rodas exceda 600 N.
113. A haste uniforme de 640m m possui uma massa de 3k g e está soldada em seu centro ao disco circular uniforme com 160m m de raio, que possui uma massa de 8k g . A unidade recebe uma velocidade de g
114. O motor elétrico possui uma massa total de 10k g e é apoiado pelos suportes de montagem A e B presos a plataforma giratória. A armadura do motor possui uma massa de 2,5k g e um raio de giração de
115. A nave espacial apresentada é simétrica em relação a seu eixo z e possui um raio de giração de 720m m em relação a esse eixo. Os raios de giração em relação aos eixos x e y através do centro de m