Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 14

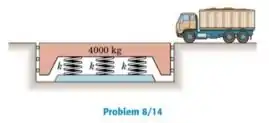
Durante o projeto do sistema de suporte de molas para a plataforma de pesagem de 4000   k g , foi decidido que a frequência de vibração livre vertical na condição descarregada não devera ser superior a três ciclos por segundo. (a) Determine a máxima constante admissível da mola k para cada uma das três molas idênticas. (b) Para essa constante de mola, qual seria a frequência natural f n da vibração vertical da plataforma carregada pelo caminhão de 40   t ?

Passo 1

A letra (a) nos dá a frequência máxima em ciclos por segundo, ou seja, precisamos expressar f n :

f n = ω n 2 π

Mas como:

ω n = 3 k m

O 3 aparece por serem três molas em paralelo

Ficamos com:

f n = 1 2 π 3 k m

Passo 2

A massa dada é a própria massa do sistema de suporte, sem nenhum peso adicional, então a equação para k será:

k = 4 m π 2 f n 2

k = 4 3 ( 4000 k g ) π 2 ( 3   H z ) 2

k = 474 k N / m

Passo 3

E para a letra (b), precisaremos apenas considerar a massa como sendo a massa do suporte mais a massa do caminhão:

m = 4000 k g + 40000 k g = 44000 k g

Pela equação da frequência, que já usamos antes:

f n = 1 2 π 3 k m

E usamos a constante elástica obtido no passo anterior, teremos:

f n = 1 2 π 3 ( 47400 N / m ) 44000 k g

f n = 0.905   H z

Resposta

( a ) k = 474 k N / m

( b ) f n = 0.905   H z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

22. O grande recipiente de cimento, suspenso pelo guindaste por um cabo elástico, possui uma massa de 4000k g . Quando o recipiente é perturbado, uma oscilação vertical com período de 0,5s é observada
28. Determine o valor do fator de amortecimento ζ para o sistema massa-mola-amortecedor simples apresentado.
24. O cilindro de massa m recebe um deslocamento vertical y 0 a partir de sua posição de equilíbrio e é solto. Escreva a equação diferencial para a vibração vertical do cilindro e determine o período
21. Uma pequena partícula de massa m está presa a dois fios muitos tensos, conforme mostrado. Determine a frequência natural ω n do sistema para pequenas oscilações verticais se a tração T em ambos os
20. Um para-choque de um automóvel que absorve energia, com suas molas inicialmente sem deformação, possui uma constante de mola equivalente de 535k N / m . Se o carro de 1200k g se aproxima de uma pa