Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 54
O elevador tem uma massa de 3000 kg quando totalmente carregado e está ligado pelo modo mostrado na figura, a um contrapeso de massa 1000 kg. Determine a potência em kW entregue pelo motor (a) quando o elevador estiver movendo-se para baixo a uma velocidade constante de 3 m/s e (b) quando ele tiver uma velocidade de 3 m/s para cima e uma desaceleração de .
Passo 1
Vamos lá! Vamos começar a questão pela letra a), que é bem fácil.
Aqui sabemos que o elevador está descendo a uma velocidade constante. Por causa disto, a potência do motor pode ser calculada através da seguinte equação:
Em que é a velocidade da corda que é puxado pelo moto e é a força do motor. Mas qual é esta força? Precisamos obtê-la! Para isto, será fundamental fazermos o diagrama de corpo livre do elevador . Desta forma, temos:
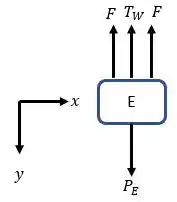
Sendo a tração que puxa o contrapeso (que é igual ao peso, pois esse não acelera) e o peso do elevador. Então, como o elevador possui aceleração nula (velocidade constante), temos:
Passo 2
Para finalizarmos a letra a), vamos ter que calcular a velocidade da corda . Pela geometria do problema (jogo de polias), se o elevador desce um comprimento , então é puxado um comprimento de da corda .
Assim, podemos afirmar que a velocidade da corda é:
E agora já podemos calcular a potência do motor, a qual será:
Passo 3
Agora vamos para a letra b). Aqui o procedimento é bastante semelhante.
A princípio, a grande diferença é que o elevador se desloca para cima, mas com uma desaceleração de (aceleração para baixo). Portanto, ao fazermos o somatório das forças, não será igual a zero.
Já o resto deverá ser o mesmo (calcular a força e multiplicar pela velocidade de 3 m/s).
Mas calma, muita calma nessa hora. Para a letra b) o contrapeso também está em aceleração, a qual é só que para cima! Portanto, a tração será:
Agora sim podemos calcular a força . Portanto,
Como a velocidade continua a mesma em módulo, então, a potência será:
E assim finalizamos a questão.