Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 58
Um furo de de diâmetro é feito em uma peça de aço de de espessura. Em seguida, o furo é escareado como mostrado na figura. Determine o volume de aço removido durante o processo de escareamento.
Passo 1
Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine o volume removido. Para isso, vamos utilizar o teorema de Pappus. Primeiro, vamos precisar calcular a distância do centroide do triângulo para o eixo de rotação. Fica assim:
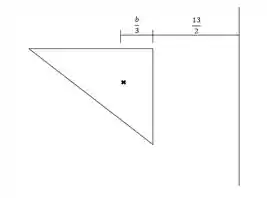
Precisamos agora encontrar a área deste triângulo:
Passo 2
Por fim, vamos usar o teorema de pappus para o volume:
Resposta
Exercícios de Livros Relacionados
Determine o volume V gerado pela revolução de 90 graus em torno do eixo z da área em forma de quarto de circulo.
A área mostrada é girada de 360 graus em torno do eixo y . Determine o volume do corpo resultante, que é uma esfera que tem uma parte significativa removida.
O tanque de armazenamento de água é uma casca de revolução e deve ser recoberto duas camadas de tinta, que dá uma cobertura de 16m 2 por galão. O engenheiro (que se lembra de mecânica) consulta um des
Determine a área superficial total A e o volume V do sólido completo mostrado na seção transversal. Determine a massa do corpo se ele for contruído de aço.
Calcule o volume V do espaçador de borracha, em forma de um anel completo, com a seção semicircular mostrada. Calcule também a área superficial A da parte externa do anel.