Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 7

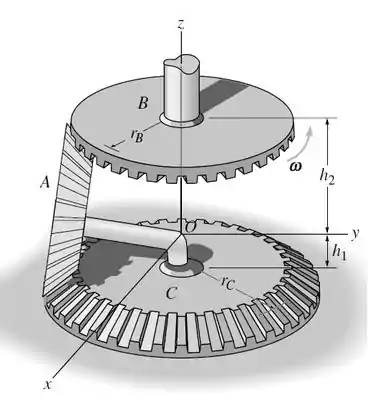
Se a engrenagem de cima B gira a uma taxa constante ω , determine a velocidade angular da engrenagem A, que está livre para girar em torno do eixo e rola sobre a engrenagem fixa de baixo C.

Passo 1

A velocidade linear em P é dada por :

v P = ω k × - r B j = ω r B i

Ou ainda por:

v P = ω A × ( - r B j × h 2 k )

v P = ω A y h 2 + ω A z r B i - ω A x h 2 j - ω A x r B k

Dessa forma pode-se equacionar as componentes i, j e k no sistema abaixo:

ω r B = ω A y h 2 + ω A z r B 0 = ω A x h 2 0 = ω A x r B (1)

Desse modo temos que :

ω A x = 0

Passo 2

A velocidade em R é dada por:

v R = 0 = i j k 0 ω A y ω A z 0 - r C - h 1 = [ - ω A y h 1 + ( - ω A z r C ) ] i

Solucionando a equação a cima:

ω A y = ω A z r C h 1

Passo 3

Da primeira equação do sistema em (1), temos que :

ω r B = ω A z r C h 2 h 1 + r B

ω A z = r B h 1 ω r C h 2 + r B h 1

ω A y = r C h 1 r B h 1 ω r C h 2 + r B h 1

Assim a velocidade angular na engrenagem A será:

ω A = r C h 1 r B h 1 ω r C h 2 + r B h 1 j + r B h 1 ω r C h 2 + r B h 1 k

Resposta

De acordo com os passos 1,2 e 3 a velocidade angular na engrenagem A será:

ω A = r C h 1 r B h 1 ω r C h 2 + r B h 1 j + r B h 1 ω r C h 2 + r B h 1 k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a estrutura gira com uma velocidade angular constante ω p = - 10 kr a d / s e a engrenagem horizontal B gira com uma velocidade angular constante ω B = 5 kr a d / s , determine a velocidade angular
No instante mostrado, o motor gira em torno do eixo z com uma velocidade angular ω 1 = 3m / s e aceleração angular ω ˙ 1 = 1,5r a d / s 2 . Simultaneamente, o eixo O A gira com uma velocidade angular
No instante θ = 30 ° , o corpo do satélite está girando com uma velocidade angular ω 1 = 29r a d / s , e tem uma aceleração angular ω ˙ 1 = 5r a d / s 2 . Simultaneamente, os painéis solares giram com
Quando a barra AB está na posição mostrada, o anel A se desloca com uma velocidade v A = { 3 i } m/s e aceleração a A = { 0,5 i } m/s2, determine a aceleração do anel B nesse instante. Suponha que a v
Se o anel A se desloca com uma velocidade constante v A = { 3 i } m / s , determine a velocidade do anel B quando a barra AB está na posição mostrada. Suponha que a velocidade angular de AB é perpendi