Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 176

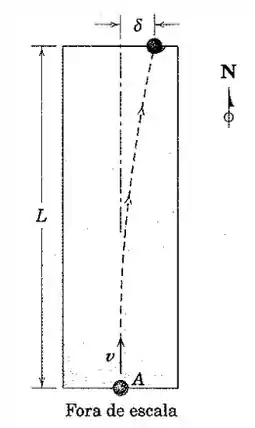
Uma pista de boliche lisa é orientada na direção norte-sul como mostrado. Uma bola A é liberada com uma velocidade v ao longo da pista conforme indicado. Em função do efeito de Coriolis, a bola desvia uma distancia δ como indicado. Desenvolva uma expressão geral para δ . A pista de boliche está localizada em uma latitude θ no hemisfério norte. Avalie sua expressão para as condições L = 18 m ,   v = 4,5 m s e   θ = 40 ° . Os jogadores de boliche devem preferir pistas orientadas na direção leste-oeste? Declare quaisquer hipóteses.

Passo 1

Bom pessoal, mais um exercício envolvendo aceleração de Coriolis. Vamos precisar da velocidade angular da Terra encontrada na tabela D/2.

ω = 7,292 × 10 - 5   k ^ r a d / s

Agora, vamos representar a posição de A em relação a Terra, como já feito no Prob.5/161.

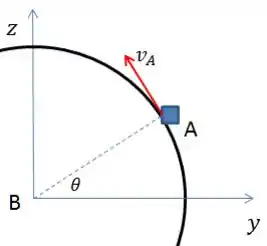
Pelo enunciado, θ = 40 ° , então a velocidade de A pode ser escrita por:

v A = v ( - s e n 40 ° j ^ + c o s 40 ° k ^ )

Por definição, a aceleração de Coriolis é dada por:

a c o r = 2 ω × v r e l

Onde v r e l é a velocidade de A em relação a um observador na pista de boliche. Então:

a c o r = 2 ω k ^ ×   v - s e n 40 ° j ^ + c o s 40 ° k ^ = 2 ω v s e n 40 ° i ^ = 2 7,292 × 10 - 5 4,5 s e n 40 i ^

a c o r = 42,2 × 10 - 5   m / s 2

Passo 2

Pronto! Agora vamos visualizar a pista de boliche e usar novas referências de eixos, em relação ao jogador.

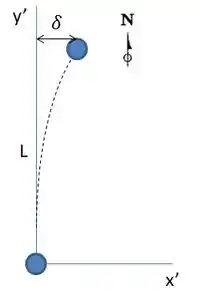
Agora, vamos usar a cinemática para descobrir o quanto a bola está sendo deslocada.

δ = 1 2 a t 2 = 1 2 a c o r L v 2 = 1 2 42,2 × 10 - 5 18 4,5 2

δ = 3,4 × 10 - 3 m = 3,4 m m

Portanto, a bola irá desviar 3,4 mm para o Leste.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carro B está contornando a curva com uma velocidade constante de 54 km/h, e o carro A está se aproximando do carro B no cruzamento com uma velocidade constante de 72 km/h. Determine a velocidade que
O disco gira em torno de um eixo fixo através de O com velocidade angular ω = 5 r a d / s e aceleração angular de α = 3r a d / s 2 no instante representado, nos sentidos indicados. O cursor A se deslo
O cursor A oscila na ranhura em torno da posição neutra O com uma frequência de dois ciclos por segundo e uma amplitude x m a x = 50 m m de modo que o seu deslocamento em milímetros pode ser escrito x
Se os carros do prob. 5/171 têm ambos uma velocidade constante de 72 km/h enquanto contornam as curvas, determine a aceleração que A parece ter para um observador se deslocando e girando com o carro B
O transporte aéreo B está voando com uma velocidade constante de 800 km/h em um arco horizontal com 15 km de raio. Quando B atinge a posição mostrada, a aeronave A, voando para sudoeste a uma velocida