Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 60

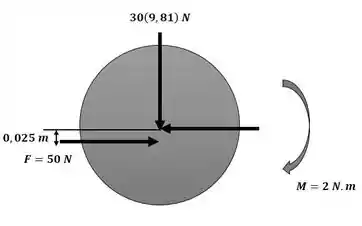
Um motor fornece um torque constante M = 2 N.m para o eixo de 50 mm de diâmetro O conectado ao centro do volante de 30 kg. O atrito resultante do mancal F, que o mancal exerce sobre o eixo, atua tangente ao eixo e tem uma intensidade de 50 N. Determine quanto tempo o torque tem de ser aplicado ao eixo para aumentar a velocidade angular do volante de 4 rad/s para 15 rad/s. O volante tem um raio de giração k O = 0,15 m em relação a seu centro O.

Passo 1

Vamos começar calculando o somatório de momentos em torno do ponto O, no entanto, primeiro devemos encontrar o valor do momento de inércia do eixo:

I O = m k O 2 = 30 0,15 2 → I O = 0,675   k g . m 2

Passo 2

Agora, calculando o somatório de momentos em torno do ponto O, conforme ilustração a seguir, conseguimos encontrar a aceleração angular:

↻ + ∑ M O = ∑ I O α

2 - 50 0,025 = 30 0,15 2 α

α = 1,11   r a d / s 2

Passo 3

Por fim, aplicando a equação da velocidade angular ao sistema podemos determinar o tempo necessário para variar a velocidade do eixo no intervalo em questão:

ω = ω 0 + a c t

15 = 4 + 1,11 t

t = 9,90   s

Resposta

t = 9,90   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A árvore AO da engrenagem cônica B gira em torno do eixo fixo O-x com uma velocidade constante N = 60 rpm na direção indicada. A engrenagem B se engrena com a engrenagem cônica C ao longo de seu cone
A haste vertical e o seu garfo vinculado giram em torno do eixo z na taxa constante Ω = 4r a d / s . Simultaneamente, a haste B gira em torno de seu eixo AO na taxa constante de w0 = 3 rad/s e o ângul
Enquanto manipula o haltere, as garras do dispositivo robótico possuem uma velocidade angular de 2 rad/s em torno do eixo OG com γ = 60 ° . Determine a aceleração angular do haltere. O conjunto inteir
O robô apresentado possui 5 graus de liberdade de rotação. Os eixos x-y-z estão presos no anel da base, que gira em torno do eixo Z com velocidade angular w1. O braço de O1O2 gira em torno do eixo x c
A árvore AO da engrenagem cônica B gira em torno do eixo fixo O-x com uma velocidade constante N = 60 rpm na direção indicada. A engrenagem B se engrena com a engrenagem cônica C ao longo de seu cone