Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 10
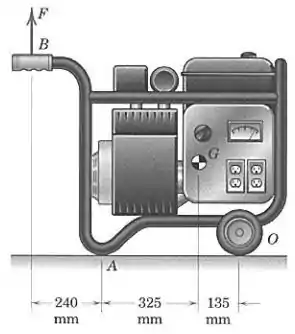
Um gerador elétrico portátil tem uma massa de , com centro de massa em . Determine a força direcionada para cima necessária para reduzir a força normal em para metade do seu valor nominal (quando .
Passo 1
Na situação de equilíbrio, a somatória dos momentos em torno de é nula. Quando , a força normal produz momento no sentido horário (negativo), enquanto o peso produz momento no sentido anti-horário (positivo):
Então, acabamos de obter o valor nominal de .
Passo 2
Agora, queremos que a força em seja metade do valor de calculado no passo anterior. Para isso, acrescentaremos o momento da força (dirigido para o sentido horário) na equação de equilíbrio de momentos em torno de :
Resposta
Exercícios de Livros Relacionados
Os elementos de um mecanismo liga-desliga de uma luminária de bancada são mostrados na figura. O interruptor S requer uma força de 4N para ser pressionado. Que força correspondente F deve ser exercida
O dispositivo mostrado é usado para testar molas de válvulas de motores de automóvel. A chave de torque está diretamente conectada ao braço O B . A especificação para a mola da válvula de admissão do
A barra uniforme O A com 18k g é mantida na posição mostrada por um pino liso em O e pelo cabo A B . Determine a força trativa T no cabo e o módulo e a direção da reação externa no pino em O .
Uma pessoa está flexionando lentamente seu braço com um peso de 10k g , como indicado na figura. O grupo de músculos braquiais (formado pelos músculos bíceps e braquial) é o principal fator nesse exer
Ao velejar com o vento a uma velocidade constante, o veleiro é impulsionado por uma força de 4k N em sua vela principal e uma força de 1,6k N em sua vela de estai, como mostrado. A resistência total d