Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 88

A estrutura é usada para sustentar o cilindro de 100 kg E. Determine as componentes horizontal e vertical da reação em A e D.

Passo 1

Desenhando o diagrama do corpo livre para os elementos DC e AC:

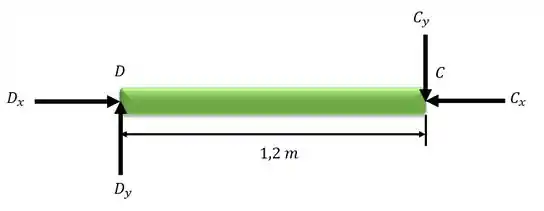
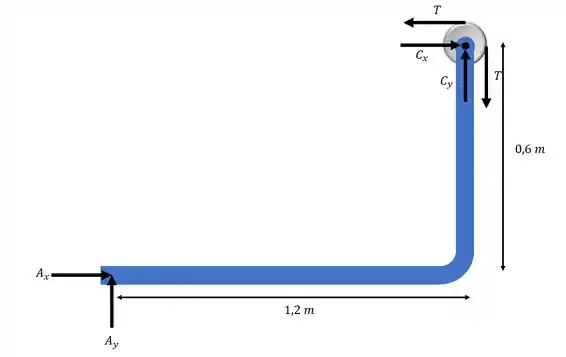
Passo 2

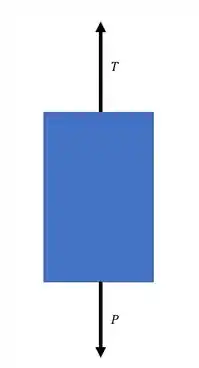
Podemos começar utilizando a equação do equilíbrio de forças no eixo y para o cilindro Σ F y = 0 T - m ⋅ g = 0 T - 100 × 9,81 = 0 T = 981   N

Passo 3

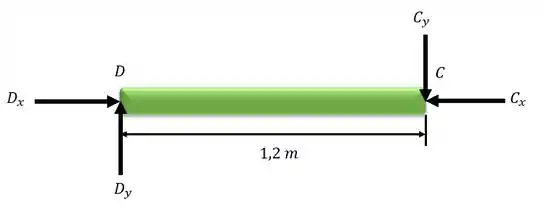
Escrevendo a equação do equilíbrio em relação ao momento para o ponto D:

Σ M D = 0 C y × 1,2 = 0   C y = 0

Passo 4

Escrevendo a equação do equilíbrio de forças nos eixos x e y :

Σ F y = 0 D y - C y = 0 D y - 0 = 0 D y = 0

Σ F x = 0 - D x - C x = 0

Passo 5

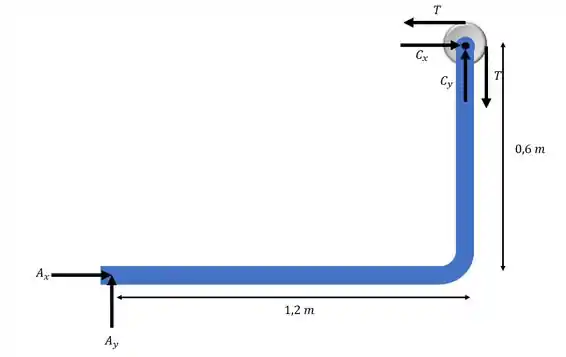
Escrevendo a equação do equilíbrio em relação ao momento para o ponto A: Σ M A = 0 C y × 1,2 - C x × 0,6 + T × 0,7 - T × 1,3 = 0 0 × 1,2 - C y × 0,6 + 981 × 0,7 - 981 × 1,3 = 0 - 0,6 C x - 588,6 = 0 0,6 C x =   - 588,6 C x = - 981   N C x = 981   N   ←

Passo 6

Escrevendo a equação do equilíbrio de forças nos eixos x e y : Σ F x = 0 A x + C x - T = 0 A x + - 981 - 981 = 0 A x - 1962 = 0 A x = 1962   N   →   Σ F y = 0 A y + C y - T = 0 A y + 0 - 981 = 0   A y = 981   N

Resposta

A x = 1962   N A y = 981   N

D x = 981   N D y = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois cabos estão ligados em C e são carregados como mostra a figura. Determine a tração ( a ) no cabo AC e ( b ) no cabo BC.
Dois cabos estão ligados em C e são carregados como mostra a figura. Sabendo que P = 500N e α = 60 ° , determine a tração (a) no cabo A C e (b) no cabo B C .
Dois cabos estão ligados em C e são carregados como mostra a figura. Sabendo que α = 20 ° , determine a tração (a) no cabo A C e (b) no cabo B C .
Uma conexão soldada está em equilíbrio sob a ação de quatro forças como mostra a figura. Sabendo que F A = 5k N e F D = 6k N , determine as intensidades das outras duas forças.
Duas forças P e Q são aplicadas tal como mostra a figura a uma conexão de uma aeronave. Sabendo que a conexão está em equilíbrio e que P = 2220N e Q = 2890N , determine as intensidades das forças exer