Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 49
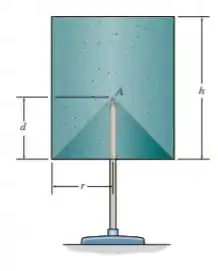
Um furo cônico é perfurado no fundo do cilindro, e depois é apoiado na barra em Determine a distância mínima a fim de que ele permaneça em equilíbrio estável.
Passo 1
Desejamos determinar uma distância mínima para mandar a peça em equilíbrio estável. Assim, vamos determinar primeiramente o centro de gravidade da combinação desse retângulo e triângulo fazendo
A energia potencial gravitacional do cilindro é positiva se o centro de gravidade se localiza acima do ponto de referência em . Assim, teremos
Então
Passo 2
Para que possamos ter o equilíbrio a condição necessária é que . Dessa forma,
Aplicando a segunda derivada para o ângulo descoberto vamos chegar em
Resposta
Exercícios de Livros Relacionados
O pêndulo de 1,5 kg oscila em relação ao eixo O - O e tem centro de massa em G . Quando θ = 0 , cada mola tem um alongamento inicial de 100 mm. Calcule a rigidez máxima k de cada uma das molas paralel
A porta de garagem uniforme A B mostrada em seção tem uma massa m e está equipada com dois mecanismos acionados por mola iguais ao mostrado, um de cada lado da porta. O braço O B tem massa desprezível
Se a energia potencial para um sistema conservativo com um grau de liberdade é expressa pela relação V = 4 x 3 - x 2 - 3 x + 10 J , onde x é dado em metros, determine as posições de equilíbrio e inves
Se a energia potencial para um sistema conservativo com um grau de liberdade é expressa pela relação V = 3 y 3 + 2 y 2 - 4 y + 50J , onde y é dado em metros, determine as posições de equilíbrio e inve
A mola tem uma rigidez k = 10k N / m e está livre quando θ = 45 º º. Se o mecanismo estiver em equilíbrio quando θ = 60 º º, determine o peso do cilindro D. Despreze o peso dos membros. A barra AB per