Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 122

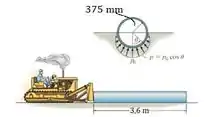
O trator é usado para empurrar o tuvo de 7,5   k N   ( ≈ 750   k g ) . Para fazer isso, ele precisa superar as forças de atrito no solo, causadas pela areia. Supondo que a areia exerce uma pressão sobre a parte inferior do tubo, conforme a figura, e o coeficiente de atrito estático entre o tubo e a areia é μ s = 0,3 , determine a força horizontal exigida para empurrar o tubo para frente. Além disso, determine a pressão de pico p o .

Passo 1

Vamos desenhar o diagrama de corpo livre dessa situação para entendermos a situação da nossa questão! Para a base do mancal, temos:

Passo 2

Essa questão não é tããão complicada, só precisamos ir com calma! Bom, se o sistema está em equilíbrio, sabemos que o somatório de forças nos eixos de referência ( x ,   y , z ) devem ser iguais a zero. Assim, vamos olhar para o diagrama de corpo livre. Assumindo como direção positiva para cima, temos:

∑ F y = 0

2 l ∫ 0 π / 2 p o c o s θ r d θ c o s θ - W = 0

2 p o l r ∫ 0 π 2 c o s 2 θ d θ = W

2 p o r l 1 2 θ + 1 4 s e n 2 θ 0 π 2 = W

2 p o r l π 4 = W

Passo 3

Agora, vamos substituir os valores na euqação anterior para encontrarmos o valor de p o !

2 p o 3,6 375 × 10 - 3 π 4 = 7500

p o = 3536,8   N / m ²

Passo 4

A força necessária para empurrar o bloco para frente é igual a:

F = ∫ - π 2 π 2 μ s d N = ∫ - π 2 π 2 0,3 p o c o s θ r l d θ

F = ∫ - π 2 π 2 0,3 3536,8 c o s θ 0,375 3,6 d θ

F = 1432,4 ∫ - π 2 π 2 c o s θ d θ

F = 1432,4 s e n θ - π 2 π 2

F = 2864,8   N

Resposta

A força horizontal exigida para empurrar o tubo para frente é igual a:

F = 2864,8   N

A pressão de pico p o é igual a:

p o = 3536,8   N / m ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O alpinista de 80 kg é abaixado por sobre a borda do penhasco por seus dois companheiros, que exercem juntos uma força horizontal T de 350 N na corda. Calcule o coeficiente de atrito μ entre a corda e
Se o marinheiro do Prob. 6/95 deve suportar uma força trativa de 18 kN na corda presa ao navio, quantas voltas em torno do mourão são necessárias se ele puxa a extremidade livre com uma força de 240 N
Para um certo coeficiente de atrito μ e um certo ângulo α , a força P necessária para elevar m vale 4 kN e a necessária para abaixar m vale 1,6 kN. Calcule a massa m .
Em filmes do Velho Oeste, frequentemente se observa os caubóis prendendo seus cavalos simplemente dando poucas voltas da rédea em torno de uma barra horizontal e deixando a extremidade pendendo livrem
Um momento no sentido anti-horário M = 150N ⋅ m é aplicado ao rotor. Se o coeficiente de atrito entre a fita e o rotor vale 0,20, calcule a força mínima P necessária para impedir a roda de girar.