Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 70
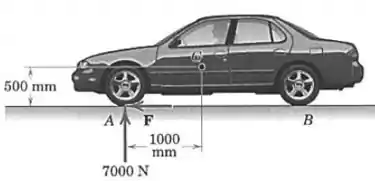
As rodas do automóvel de tração dianteira sofrem, em conjunto, a ação de uma força de reação normal de e de uma força de fricção , ambas exercidas pela superfície da estrada. Se é sabido que a resultante destas duas forças faz um ângulo de com a vertical, determine o sistema força-binário equivalente no centro de massa do carro. Trate este problema como sendo bidimensional.
Passo 1
Vamos começar somando vetorialmente essas duas forças que agem sobre o pneu do carro:
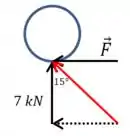
E podemos usar isso para determinar o módulo da força :
Passo 2
Agora queremos determinar o sistema força-binário em que é equivalente a essa força resultante.
A força do nosso sistema deve ser igual à própria força resultante (a seta vermelha no nosso desenho), só que deslocada até o ponto :
E precisamos descobrir o momento dessa força em relação a quando ela está em sua posição original.
Passo 3
Nós já temos os dois componentes da força , agora só precisamos calcular o momento associado a cada uma dessas componentes:
Olhando para a imagem do enunciado, podemos ver que:
E então:
E esse momento favorece a rotação no sentido horário.
Resposta
A força deve ser e o binário deve ser no sentido horário.