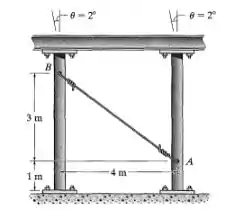
Originalmente, o cabo de ancoragem AB de uma estrutura de edifício não está esticado. Devido a um terremoto, as duas colunas da estrutura inclinam-se até um ângulo θ = 2º. Determine a deformação normal aproximada do cabo quando a estrutura estiver nessa posição. Considere que as colunas são rígidas e giram ao redor de seus apoios inferiores.
Passo 1
Olá, querido! Cê tá bem? Então, ele quer saber a deformação normal de se as colunas rotacionarem em relação aos seus apoios, algo assim:
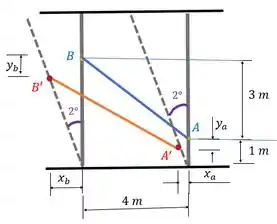
Olhando a figura a gente deve perceber que , por estar mais afastado das bases, sofrerá um deslocamento maior do que .
Bem, a fórmulinha da deformação normal é
Onde é o comprimento inicial do cabo e é comprimento depois da rotação. Então para achar a deformação a gente precisa achar essas duas coisinhas.
A ideia aqui é usar alguns conhecimentos de geometria para achar esses caras e daí achar a deformação. Bora ver como!
Passo 2
Vamos começar achando o comprimento . Da figura a gente cosegue tirar esse triânguo retângulo:

Ele é um triângulo 3/4/5, então temos que . Cê poderia chegar nesse resultado usando Pitagoras também, tá?
Passo 3
Agora vamos achar o comprimento do cabo deformado . Aqui a gente vai achar a projeção desse cabo na hozizontal e depois achar a projeção dele na vertical . Aí para achar o comprimento do cabo mesmo, a gente faz:
Vamos olhar nossa figura novamente:

A gente tem que e podem ser escritos em função dos deslocamentos do ponto e do ponto , como colocamos na figura. Os pilares não mudam de tamanho, por isso a distância entre um ponto e a base do seu pilar permanece a mesma.
Vamos olhar para o ponto .
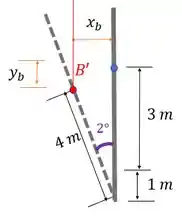
vai ser a projeção do pilar inclinado até na horizontal. Como o ângulo está oposto ao eixo horizontal, a gente vai usar o seno aqui
Já vai ser os menos a projeção da coluna na vertical
Passo 4
Agora olhando para :

Daí a gente tira que é a projeção da coluna até na horizontal:
E para
Passo 5
Aí a gente consegue achar e . Vimos antes que eles valem:
Substituindo o que a gente achou e calculando:
E na horizontal:
Aí o comprimento novo do cabo é
Passo 6
Podemos agora utilizar os comprimentos iniciais e finais para determinarmos a deformação: