Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 3.Problemas - Ex. 41
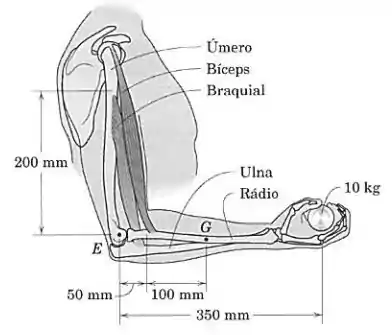
Uma pessoa está flexionando lentamente seu braço com um peso de , como indicado na figura. O grupo de músculos braquiais (formado pelos músculos bíceps e braquial) é o principal fator nesse exercício. Determine o módulo da força do grupo de músculos braquiais e o módulo da reação do cotovelo no ponto , para a posição do antebraço mostrada na figura. Use as dimensões mostradas para localizar os pontos efetivos de aplicação dos dois grupos de músculos; esses pontos estão diretamente acima de e diretamente à direita de . Inclua o efeito da massa de do antebraço, que tem centro de massa no ponto . Descreva qualquer hipótese feita.
Passo 1
Vamos assumir que o ponto de aplicação da força está à direita de , na mesma linha horizontal de . Sendo assim, essa força faz um ângulo com a vertical, calculado assim:
Assim, em torno de , a componente de que causará momento será a vertical , a de (sentido anti-horário ou positivo), além dos dois pesos (sentido horário ou negativo). Então, temos:
Passo 2
Através da equação de equilíbrio de forças na horizontal, podemos calcular a componente da força em :
Passo 3
Agora, usando a equação de equilíbrio de forças na vertical, calculamos a componente da força em :
Logo,