Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 137

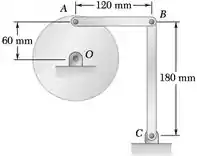
A haste AB de 2 kg e a haste BC de 3 kg estão ligadas, como mostra a figura, a um disco que é colocado em rotação em um plano vertical. Sabendo que no instante mostrado na figura o disco tem uma aceleração angular de 18 rad/s no sentido horário e velocidade angular nula, determine os componentes das forças aplicadas em A e B sobre a haste AB.

Passo 1

Cinemática:

Velocidade de todos os elementos = C

Aceleração:

a B = a A = 0.25   ft 18   rad/ s 2 = 4.5   ft/ s 2 →

α B C = a B 0.75   ft = 4.5   ft/ s 2 0.75   ft

α B C = 6   rad/ s 2  

a - B C = 0.375   ft 6   rad/ s 2 = 2.75   ft/ s 2 →

a - A B = a A = a B = 4.5   ft/ s 2 →

Passo 2

Cinética:

I - B C = 1 12 m B C B C 2 = 1 12 6   lb 32.2 0.75   ft 2

Passo 3

Haste BC:

I - B C = 8.734 × 10 - 3   lb ∙ ft ∙ s 2

+ Σ M A = Σ M A eff:             B y 0.75   ft = I - B C α B C + m B C a - B C 0.375   ft

0.75 B y = 8.734 × 10 - 3   lb ∙ ft ∙ / s 2 6   rad/ s 2

+ 6   lb 32.2 2.25   ft/ s 2 0.375   ft

0.75 B x = 0.0524 + 0.1572

B x = 0.2795   lb

(em AB)

Resposta

B x = 0.280   lb ←

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga esbelta de 3m possui uma massa de 50k g e é liberada a partir do repouso na posição horizontal em θ = 0 . Se o coeficiente de atrito estático entre o suporte fixo junto a O e a viga é de 0,30 ,
11. Se a barra AB desliza ao longo da ranhura horizontal com uma velocidade de 18 m/s, determine a velocidade angular da barra de ligação BC no instante mostrado.
Para o instante representado, o centro instantâneo de velocidade nula para a placa retangular em movimento plano está localizado em C. Se a placa possui uma velocidade angular no sentido anti-horário
A placa retangular gira em torno de seu eixo fixo z. No instante considerado sua velocidade angular é ω = 3r a d / s e está diminuindo na taxa de 6 rad/s por segundo. Para esse instante escreva as exp
O grande carretel para cabo de eletricidade é rolado para cima no plano inclinado pelo veículo conforme mostrado. O veículo parte do repouso com x = 0 para o carretel e acelera na taxa constante de 0,