Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.3 - Ex. 54

54. O bloco de massa m = 45   k g é suspenso por duas molas, cada uma com rigidez k = 3   k N / m , e está sob a ação da força F = 350 ⋅ cos ⁡ 15 t   N onde t é o tempo em segundos. Determine a amplitude X do movimento em regime permanente se o coeficiente de amortecimento viscoso é c é

(a) 0 e

(b) 900   N ⋅ s / m

Compare essas amplitudes com a deflexão estática das molas δ .

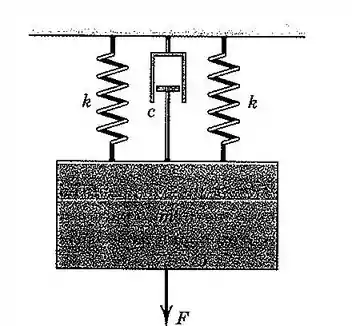
Passo 1

Bom, primeiramente temos que lembrar que a fórmula de frequência natural do sistema tem a seguinte cara:

ω n = k m

Onde k é a constante elástica da mola e m a massa do corpo. Aqui, devemos multiplicar o k por 2 , pois há duas molas.

ω n = 2 ( 3000 N / m ) 45   k g

ω n = 133,333

ω n ≅ 11,55   r a d / s

Passo 2

(a) Agora, lembraremos a fórmula de amplitude X para o coeficiente de amortecimento viscoso c = 0   N ⋅ s / m :

X = F 0 / k 1 - ω ω n 2

Onde F 0 é a força inicial de excitação e ω a frequência de vibração da força, que é dado pelo valor que acompanha o t no argumento da função c o s na equação de força. De modo que substituindo os valores numéricos, obtemos que:

X = ( 350   N ) / 2 ( 3000 N / m ) 1 - 15 11,55 2

X = 0,0583 1 - 1,298 2

X = 0,0583 1 - 1,684

X = 0,0583 - 0,684

X = 0,0853   m

Passo 3

(b) Para um movimento com um amortecimento, devemos usar a fórmula:

X = F 0 / k 1 - ω ω n 2 2 + 2 ζ ω ω n 2

Onde o fator de amortecimento ζ é dado pela fórmula abaixo:

ζ = c 2 m ω n

ζ = 900   N ⋅ s / m 2 ( 45   k g ) ( 11,55 r a d / s )

ζ = 0,866

E agora, substituindo esse valor na fórmula da amplitude:

X = ( 350   N ) / 2 ( 3000 N / m ) 1 - 15 11,55 2 2 + 2 ( 0,866 ) ( 15 ) ( 11,55 ) 2

X = 0,0583 1 - 1,298 2 2 + 2,249 2

X = 0,0583 1 - 1,684 2 + 5,059

X = 0,0583 - 0,684 2 + 5,059

X = 0,0583 0,468 + 5,059

X = 0,0583 5,527

X = 0,0583 2,351

X = 0,0248   m

Passo 4

A amplitude de deflexão estática δ , cuja fórmula se assemelha muito a da deformação elástica, e não precisa nem explicar o porquê, será dada por:

δ = P ( F o r ç a ) k ( C o n s t a n t e )

Onde P é o valor do peso do bloco:

δ = ( 45   k g ) ( 9,81 m / s 2 ) 2 ( 3000 N / m )

δ = 441,45 6000

δ = 0,0736   m

E a caráter de comparação, podemos observar que quanto menos amortecimento, mais a deflexão estática encontra-se próxima da amplitude X :

Resposta

(a) A amplitude X será:

X = 0,0853   m

(b) A amplitude X será:

X = 0,0248   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

62. A unidade motorizada de 20k g com velocidade variável é limitada na direção horizontal por duas molas, cada uma das quais possui uma rigidez de 2,1k N / m . Cada um dos dois amortecedores possui u
48. Determine a amplitude X do movimento em regime permanente da massa de 10k g se (a) c = 500N ⋅ s / m e(b) c = 0 .
61. O movimento do carrinho externo B é dado por x B = b ⋅ s e n ω t . Para qual faixa da frequência d excitação ω , a amplitude do movimento da massa m em relação ao carrinho é inferior a 2 b ?
96. O “boneco” segmentado do Prob. 6 / 107 é reapresentado aqui. Assume-se que articulação do quadril O permanece fica em relação ao carro, e o tronco acima do quadril é considerado como um corpo rígi
97. Os elementos da suspensão traseira independente, do tipo “eixo-flutuante”, para automóveis são representados na figura. O diferencial D está firmemente fixado ao chassi do carro. Os semieixos são