Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas Fundamentais - Ex. 25
Substitua o carregamento do sistema por uma força e momento de binário resultante equivalente agindo no ponto .
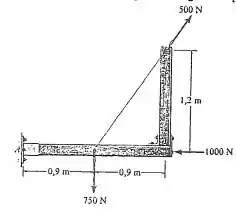
Passo 1
A questão pede para substituirmos todas as forças do problema por uma força resultante e um momento de binário resultante com relação ao ponto . Para isso, o primeiro passo é decompor as forças:
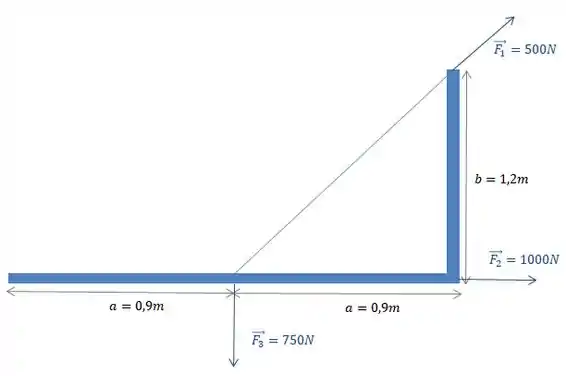
Onde , , , e .
Para a força tivemos que fazer a decomposição nas direções e , daí apareceram senos e cossenos em função de e . Substituindo os valores a gente tem:
E aí:
Desta forma, a força resultante é:
Passo 2
Para o binário, basta calcular o momento de cada força com relação ao ponto e somar cada um. Lembrando a definição de momento:
Neste caso, temos que
Assim,
Somando todos os momentos:
Resposta
Exercícios de Livros Relacionados
Calcule o módulo da força trativa T → e o ângulo θ de forma que o olhal tenha uma força resultante de 15k N direcionada para baixo.
Determine a resultante R → das quatro forças atuando na placa de união. Ache também o módulo de R → e o ângulo θ x que a resultante faz com o eixo x .
Determine a altura h acima da base B na qual atua a resultante das três forças.
Determine o módulo da força F → aplicada à manopla que fará com que a resultante das três forças passe por O .
Sob condições não uniformes e escorregadias da estrada, as duas forças mostradas são exercidas sobre as duas rodas de tração traseiras da caminhonete, que tem um diferencial traseiro que limita derrap