Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 83

No instante mostrado, duas forças atuam sobre a barra fina de 15 kg que está presa com pino em O. Determine a intensidade da força F e a aceleração angular inicial da barra, de maneira que a reação horizontal que o pino exerce sobre a barra seja 25 N direcionada para a direita.

Passo 1

Iremos considerar a aceleração da gravidade g = 9,81   m / s 2 .

Começaremos o exercício calculando o momento de intércia da barra com relação ao ponto O:

I O = 1 12 m r G 2 + m d 2 = 1 12 15 2,4 2 + 15 1,2 2

I O = 28,8   k g . m 2

No instante mostrado, a componente tangencial da aceleração do centro de massa da barra:

a G t = α r g = 1,2 α

Passo 2

Agora iremos aplicar o somatório de momentos em torno do ponto O com o auxílio do diagrama a seguir:

- 100 0,9 - F 1,8 = - 28,8 α

F = - 50 + 16 α

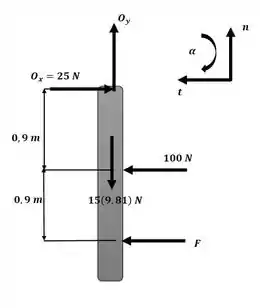
Essa será nossa equação número 1. Agora iremos aplicar o somatório de forças na direção tangencial:

+ ←   ∑ F t = m a G t

100 + F - 25 = ( 15 ) ( 1,2 α )

Essa será nossa equação número 2.

Passo 3

Agora iremos substituir a equação 1 na equação 2:

100 + - 50 + 16 α - 25 = 15 1,2 α

α = 12,5   r a d / s 2

Agora, substituindo na equação 1 para encontrar o valor de F:

F = - 50 + 16 ( 12,5 )

F = 150   N

Resposta

α = 12,5   r a d / s 2

F = 150   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco circular de 6 kg e o eixo associado giram a uma velocidade angular constante ω = 10000r p m . Se o centro de massa do disco está deslocado do centro em 0,05 mm, determine o módulo das forças h
A haste esbelta uniforme d comprimento l está soldada ao suporte em A na parte inferior do disco B . O disco gira em torno de um eixo vertical com uma velocidade angular constante ω que resultará em u
Se a barra semicircular do Prob. 7/81 parte do repouso sob a ação de um torque M o aplicado através do anel em torno de seu eixo de rotação z, determine o momento fletor inicial M na barra em A.
Determine o momento fletor M no ponto de tangência A na barra semicircular de raio r e massa m , enquanto a barra gira em torno do eixo tangente com uma velocidade angular constante e elevada ω . Desp
Resolva o Probl. 7/85 para o caso em que o conjunto parte do repouso com uma aceleração angular inicial α = 900r a d / s 2 como resultado de um torque de partida(binário) M aplicado á haste no mesmo s