Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 85

A massa da barra esbelta uniforme é de 3   k g . Determine a posição x para o cursor de 1,2   k g de tal modo que o período do sistema seja de 1   s . Assuma pequenas oscialções em torno da posição de equilíbrio horizontal mostrada.

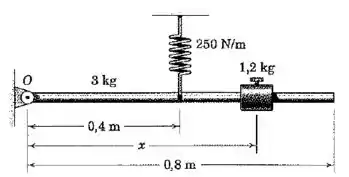
Passo 1

Conforme o cursor de 1,2   k g se move, o momento de inércia do sistema varia. Vamos procurar uma expressão que descreva essa variação:

I O = 1 3 m L 2 + 1,2 x 2

I O = 1 3 3 L 2 + 1,2 x 2 = L 2 + 1,2   x 2

E então podemos montar uma equação de momentos em torno do ponto O :

∑ M O = I O θ ¨

E a única força que produz oscilação em torno de O é a força elástica da mola presa em L / 2 :

∑ M O = - k L 2 sen ⁡ θ L 2 cos ⁡ θ

∑ M O = - k L 2 4 sen ⁡ θ cos ⁡ θ

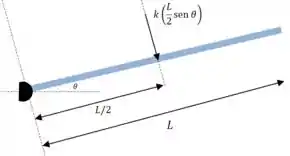
Passo 2

Agora vamos substituir tudo isso na equação principal:

∑ M O = I O θ ¨

- k L 2 4 sen ⁡ θ cos ⁡ θ = L 2 + 1,2   x 2 θ ¨

E podemos aproximar sen ⁡ θ ≅ θ e cos ⁡ θ ≅ 1 :

- k L 2 4 θ = L 2 + 1,2 x 2 θ ¨

Então:

θ ¨ + k L 2 4 L 2 + 1,2 x 2 θ = 0

Então a frequência angular é:

ω 2 = k L 2 4 L 2 + 1,2 x 2

E o período é:

τ = 2 π ω = 2 π   4 L 2 + 1,2 x 2 k L 2

Passo 3

Queremos calcular o valor de x para que τ = 1   s , então:

2 π   4 L 2 + 1,2 x 2 k L 2 = 1

Vamos substituir os valores numéricos:

4 π   0,8 2 + 1,2 x 2 250 0,8 2 = 1

Elevando os dois lados ao quadrado:

16 π 2   0,8 2 + 1,2 x 2 250 0,8 2 = 1

1,2 x 2 = 0,3732

x = 0,558   m

Resposta

Para que o período seja de 1 s, é preciso ter x = 0,558   m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sistema do Prob. 8/46 é repetido aqui. Se a barra curva A B possui agora uma massa m 2 e um raio de giração k O em relação ao ponto O , determine expressões para a frequência natural não amortecida
O sistema do Prob. 8/45 é repetido aqui. Se o elemento de ligação A B possui agora uma masssa m 3 e um raio de giração k O em relação ao ponto O , determine a equação do movimento em termos da variáve
Determine a frequência natural f n para pequenas oscilações do corpo composto no plano vertical em torno do mancal O . Aproxime o corpo como uma barra esbelta de massa m / 5 e um disco semicircular de
O disco circular de massa m e momento de inércia I , em relação a seu eixo central, está soldado ao eixo de aço, que, por sua vez, está soldado ao bloco fixo. O disco recebe um deslocamento angular θ