Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 95
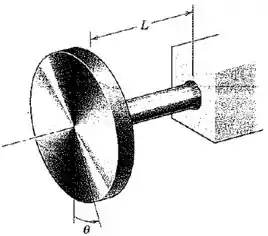
O disco circular de massa e momento de inércia , em relação a seu eixo central, está soldado ao eixo de aço, que, por sua vez, está soldado ao bloco fixo. O disco recebe um deslocamento angular e em seguida é liberado, provocando uma vibração torcional do disco com variando entre e . O eixo resiste à torção com um momento , onde é o momento polar de inércia da seção transversal do eixo em relação ao eixo de rotação, é o módulo de elasticidade transversal do material do eixo (relação entre tensão e deformação de cisalhamento), é o ângulo de torção em radianos, e é o comprimento do eixo sob torção. Desenvolva a expressão para a frequência natural da vibração torcional.
Passo 1
Esse problema é mais mais simples do que parece: o enunciado já deu a expressão para o momento resultante em relação ao eixo!
Só precisamos adicionar o sinal negativo, notando que o momento favorece o retorno do ângulo ao ponto de equilíbrio.
O enunciado também deu o momento de inércia , então nem sequer precisamos encontrar uma expressão para ele. Vamos apenas reorganizar essa equação:
Passo 2
Nessa última equação, o termo que multiplica o é o quadrado da frequência angular natural do oscilador:
E a frequência pode ser calculada diretamente a partir disso:
Então:
Resposta
A frequência natural é .