Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 40
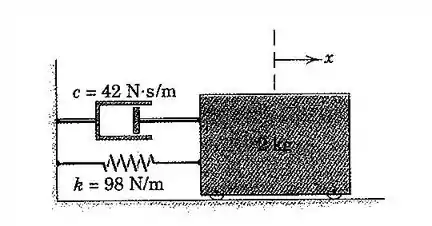
40. A massa de é liberada a partir do repouso a uma distância à direita da posição de equilíbrio. Determine o deslocamento como uma função do tempo.
Passo 1
Primeiramente, dado que temos a nossa mola com constante elástica ; o que temos que fazer é determinar a frequência angular natural do nosso sistema, que é dada pela seguinte relação abaixo:
E substituindo os valores numéricos pertencentes a cada variável, chegamos à:
Passo 2
E agora, vamos lembrar que o fator de amortecimento está relacionado com a frequência natural e o coeficiente de amortecimento viscoso pela seguinte fórmula:
Substituindo os valores numéricos que já temos, obtemos que:
Partindo desse fator de amortecimento, é que vamos obter as relações que queremos para descrever a fórmula da posição , a qual vai ser dada pela fórmula da equação amortecida para vibração livre amortecida, descrita por:
Onde e são dadas pela seguinte fórmula:
E obtemos dois valores para nosso , um máximo e outro mínimo :
De forma que nossa equação de posição fica com o seguinte aspecto:
Passo 3
Agora vamos parar um pouco pra analisar a equação de posição .
No instante inicial , a posição inicial é dada por nada mais nada menos do que a soma da amplitude com.
E a velocidade nesse instante de tempo é igual à zero! O que isso quer dizer? Ora bolas! Se derivarmos em relação ao tempo e depois igualarmos a zero, é bem capaz de obtermos outra relação entre e . Quer ver só?
Só que a nossa velocidade nesse instante de tempo inicial é igual à zero! Ou seja:
E finalmente chegamos ao seguinte sistema, com duas equações e duas incógnitas:
Vamos resolvê-lo:
E consequentemente:
Aleluia! Só falta agora, substituir e na nossa equação de posição :
Pronto! Resposta Encontrada.