43. A massa do sistema apresentado é liberada a partir do repouso em , quando Determine o deslocamento em , se (a) e (b) .
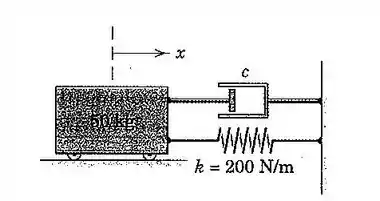
Passo 1
Primeiramente, vamos tratar de obter a frequência natural do nosso sistema, a qual é dada em função da massa e da constante elástica da mola, por:
E substituindo os valores numéricos pertinentes a cada variável, chegamos à:
Passo 2
(a) Obtida a nossa frequência angular, devemos lembrar que o fator de amortecimento é dado em função do coeficiente de amortecimento viscoso e da frequência angular natural , pela seguinte fórmula:
A questão nos fornece que . E susbtituindo os valores das outras variáveis, obtemos que:
Como o fator de amortecimento é igual a , trata-se de uma situação de amortecimento crítico, cuja equação de movimento é dada por:
O valor de nós já temos, que é a posição inicial em que o corpo é liberado, igual a . E o valor de obviamente vai ser o dobro de , uma vez que a diferença entre e é que vai nos fornecer a amplitude do movimento do nosso bloco, a qual também é igual a . Logo, nossa equação de movimento pode ser reescrita como:
Agora só falta substituir o valor do tempo que nos é fornecido, igual a :
Passo 3
(b) De novo repetimos o mesmo procedimento da letra (a), em que obtida a nossa frequência angular, devemos lembrar que o fator de amortecimento é dado em função do coeficiente de amortecimento viscoso e da frequência angular natural , pela seguinte fórmula:
A questão nos fornece nessa letra, que . E susbtituindo os valores das outras variáveis:
Xiiii! Deu ruim! O nosso fator de amortecimento é maior que o , portanto o movimento é superamortecido. De forma, que a nossa equação de posição tem a seguinte cara:
Só que uma vez que nosso é a posição inicial em que o corpo é liberado; usando proporção entre e , podemos reescrever e como:
E e nos são dadas pela seguinte fórmula:
Com isso obtemos dois valores para nosso , um máximo e outro mínimo :
Agora, só falta substituir os valores que já temos, inclusive o tempo igual a , para a equação de posição e com isso, achar nosso resultado:
Resposta
(a)
(b)