Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 134

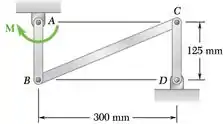
O mecanismo articulado ABCD é formado pela união da barra BC de 3 kg às barras AB e CD de 1,5 kg cada. O movimento do mecanismo é controlado pelo binário M aplicado à barra AB. Sabendo que no instante mostrado na figura a barra AB tem uma velocidade angular de 24 rad/s no sentido horário e aceleração angular nula, determine (a) o binário M, (b) os componentes da força exercida em B sobre a haste BC.

Passo 1

Cinemática:

Barra BC:

β = tan - 1 5 12

β = 22.62 °

a G / B t = B G α B C = 0.325 2 m α B C = 0.1625 α B C ↘  

a G / B t = B C α B C = 0.325 m α B C = 0.325 α ↘

a C = a B + a C / B t ;               a C x + a C y = a B + a C / B t

0.125 α C D → + 72   m/ s 2 ↓ = 72   m/ s 2 ↑ + 0.325 α B C  

+ ↓ 72 = - 72 + 0.325 α B C 12 13 ;               α B C = 480   rad/ s 2

→ + 0.125 α C D = 0.325 480 5 13 ;               α C D = 480   r a d / s 2  

a - = a B + a G / B = a B + a G / B t = 72   m/ s 2 ↑ + 0.1625 α B C  

= 72   m/ s 2 ↑ + 0.1625 480  

a - = 72   m/ s 2 ↑ + 78   m/ s 2  

→ a - x = 78 5 13 = 30   m/ s 2 →

+ ↑ a - y = 72 - 78 12 13 = 72 - 72 = 0

Passo 2

A aceleração total de G é 30   m/ s 2   →

Barra CD:

Cinemática:

[

a - C D x = 0.0625   m 480   rad/ s 2 = 30   m/ s 2 →

Passo 3

Cinética:

I - C D = 1 12 m C D 2 = 1 12 1.5   kg 0.125   m 2

I - C D = 1.953 × 10 - 3   kg ∙ m 2

+ Σ M D = Σ M D eff:             C x 0.125   m = I - α C D + m a - C D x 0.0625   m

0.125 C x = 1.953 × 10 - 3   kg ∙ m 2 480   rad/ s 2

+ 1.5   kg 30   m/ s 2 0.0625   m

0.125 C x = 3.75

C x = 30   N

Passo 4

Barra BC:

I - B C = 1 12 m B C 2 = 1 12 3   kg 0.325   m 2 = 26.406 × 10 - 3   kg ∙ m 2

m B C a - = 3   kg 30   m/ s 2 = 90   N →

→ + Σ F x = Σ F x eff :               B x - C x = m B C a -

B x - 30   N = 90   N

B x = + 120   N

+ Σ M C = Σ M C eff:             B y 0.3   m - B x 125   m - W 0.15   m

= I - B C α B C - m B C a - 0.0625   m

0.3 B y - 120 0.125 - 3 9.81 0.15 = 26.406 × 10 - 3   kg ∙ m 2 480   rad/ s 2

- 90   N 0.0625

0.3 B y - 15 - 4.4145 = 12.675 - 5.625

0.3 B y = 26.465

B y = + 88.22   N

Passo 5

Barra AB:

Cinética:

+ Σ M A = Σ M A eff:             M + B x 0.125   m = 0

M + 120   N 0.125   m = 0

M = - 15   N ∙ m

Resposta

B x = 120   N →

B y = 88.2   N ↑

M = 15   N ∙ m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco semicircular de massa m e raio r é liberado a partir do repouso em θ = 0 e gira livremente no plano vertical em relação ao seu mancal fixo em O . Desenvolva expressões para as componentes n e
O disco B possui uma massa de 22k g e um raio de giração centroidal de 200m m . A unidade de potência C é composta por um motor M e um disco em A , que é acionado a uma velocidade angular constante de
A chapa em ângulo reto é fabricada a partir de uma chapa plana com massa ρ por unidade de área e está soldada no eixo horizontal montado no mancal em O . Se o eixo é livre para girar, determine a acel
Cada uma das hastes esbeltas uniformes de massa m está soldada na sua extremidade em uma posição tangente à borda do disco circular. O disco gira em um plano horizontal em torno de um eixo vertical fi
O dispositivo robótico é composto pela base estacionária O A , o braço articulado em A , e o braço B C articulado em B . Os eixos de rotação são perpendiculares ao plano da figura. Calcule (a) o momen