Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 149

O pino B na engrenagem desliza livremente ao longo da ranhura no membro AB. Se o centro da engrenagem O se desloca com a velocidade e a aceleração mostradas, determine a velocidade angular e a aceleração angular do membro nesse instante.

Passo 1

Começaremos o exercício localizando a posição do centro instantâneo de velocidade nula do sistema conforme o diagrama a seguir:

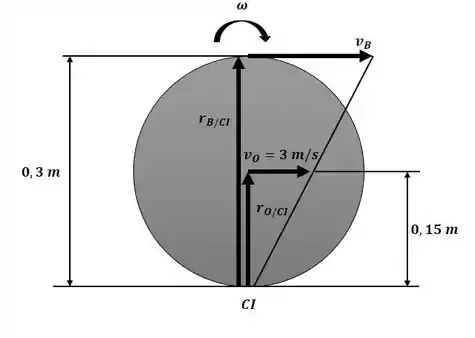
Com isso podemos encontrar a velocidade angular:

ω = v O r O / C I = 3 0,15 → ω = 20   r a d / s

E então a velocidade linear no ponto B:

v B = ω r B / C I = 20 0,3 → v B = 6   m / s

Podemos também encontrar a aceleração α da engrenagem:

α = a O r = 1,5 0,15 → α = 10   r a d / s 2

Com isso podemos aplicar a equação da aceleração com relação aos pontos B e O com o auxílio do diagrama a seguir:

a → B = a → O + α × r → B / O - ω 2 r → B / O

a B t i → - a B n j → = 1,5 i → + - 10 k → × 0,15 j → - 20 2 ( 0,15 j → )

a B t i → - a B n j → = 3 i → - 60 j →

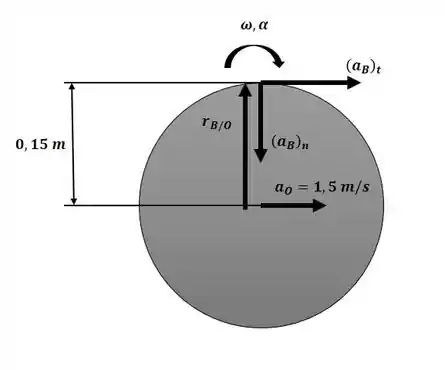
Igualando as componentes, obtemos:

a B t = 3   m / s 2

a B n = 60   m / s 2

Passo 2

Agora vamos definir nosso eixo de rotação de referência no membro AB que também coincide com o eixo na na referência fixa conforme o diagrama a seguir:

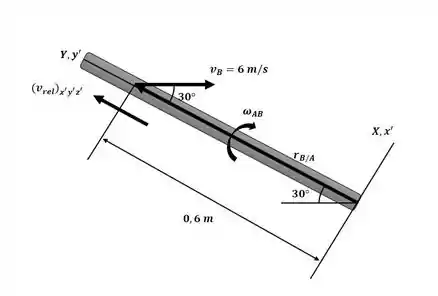
Agora iremos aplicar a equação da velocidade relativa para os pontos A e B:

v → B = v → A + Ω × r → B / A + v → r e l x ' y ' z '

3 i → - 5,196 j → = 0 + - ω A B k → × 0,6 j → + v r e l x ' y ' z ' j →

3 i → - 5,196 j → = 0,6 ω A B i → + v r e l x ' y ' z ' j →

Igualando as componentes i e j, temos:

v r e l x ' y ' z ' = - 5,196   m / s

ω A B = 5   r a d / s

Passo 3

Agora iremos aplicar a equação da aceleração relativa para os pontos A e B com base no diagrama a seguir:

a → B = a → A + Ω ˙ A B × r → B / A + Ω A B × Ω A B × r → B / A + 2 Ω A B × v r e l x ' y ' z ' + a r e l x ' y ' z '

- 50,46 i → - 32,6 j → = 0 + - α A B k → × 0,6 j → + - 5 k → × ( 0,6 j → ) ] + 2 ( - 5 k → ) × ( - 5,196 j → ) + ( a r e l ) x ' y ' z ' j →

- 50,46 i → - 32,6 j → = 0,6 α A B - 51,96 i → + [ a r e l x ' y ' z ' - 15 ] j →

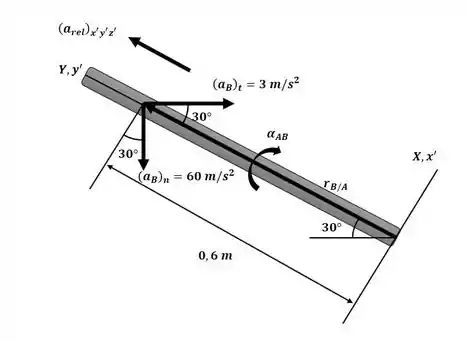
Igualando as componentes na direção i:

- 50,46 = 0,6 α A B - 51,96 → α A B = 2,5   r a d / s 2

Resposta

ω A B = 5   r a d / s

α A B = 2,5   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bola C se desloca com uma velocidade de 3 m/s, que está aumentando a uma taxa constante de 1,5 m/s2, ambas medidas em relação à placa circular e direcionadas como mostrado. No mesmo instante, a plac
A bola C se desloca ao longo da ranhura de A para B com uma velocidade de 0,9 m/s e aceleração de 0,45 m/s2, ambas medidas em relação à placa circular. Nesse mesmo instante, a placa gira com a velocid
Determine a velocidade angular e acelaração angular da placa CD do mecanismo triturador de pedras no instante em que AB está na horizontal. Neste instante, θ = 30 ° e ϕ = 90 ° . O membro de acionament
Um homem está parado na plataforma em O e corre para fora na dreção da beira da plataforma de tal maneira que, quando eles está em A, y=1,5m, seu centro de massa tem uma velocidade de 0,6 m/s e uma ac
O raio do pino B fixo à manivela AB desliza livremente ao longo da ranhura no membro CDE. Se AB gira com o movimento mostrado, determine a velocidade angular de CDE no instante mostrado.