Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 57
Resolva o problema usando o princípio de energia potencial. Investigue a estabilidade da barra quando ela está na posição de equilíbrio.
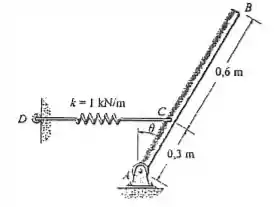
Passo 1
Utilizando o princípio a energia potencial temos
O equilíbrio ocorre quando
Avaliando a segunda derivada e aplicando os nossos pontos percebemos que é um ponto de equilíbrio estável e é um ponto de equilíbrio instável.
Resposta
Exercícios de Livros Relacionados
55- A conexão uniforme A B tem massa m e sua extremidade esquerda A desliza livremente no rasgo horizontal fixo. A extremidade B está presa ao êmbolo vertical, que comprime a mola quando B está presa
50- O sistema formado por uma barra leve articulada, a massa m da extremidade e a mola de rigidez k são mostrados em sua posição de equilíbrio. O parâmetro n é uma fração situada na faixa 0n1 . Mostre
51- Uma extremidade da mola de torção está presa ao chão em A e a outra extremidade está presa ao eixo em B . A rigidez a torção K da mola elástica é o torque necessário para torcer a mola de um ângul
57- A figura mostra uma cadeira reclinável de escritório juntamente com um detalhe do projeto do mecanismo de inclinação suportado por uma mola. A estrutura do assento é articulada em relação ao ponto
56- Determine por meio de cálculos se o semicilindro homogêneo e a casca semicilíndrica permanecerão nas posições mostradas ou se eles rolarão sobre os cilindros inferiores.