Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 3.Problemas - Ex. 42

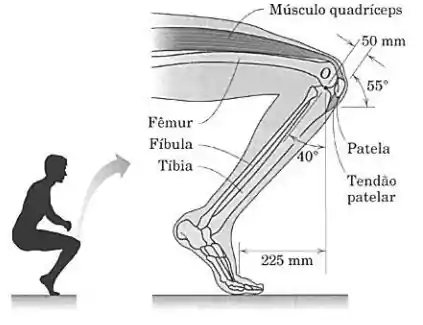
Com seu peso igualmente distribuído em ambos os pés, um homem começa a levantar-se lentamente da posição de cócoras como indicado na figura. Determine a força trativa no tendão patelar e o módulo da força de reação no ponto , que é a área de contato entre a tíbia e o fêmur. Observe que a linha de ação da força do tendão patelar ocorre ao longo de sua mediatriz. Despreze o peso da parte inferior da perna.

Passo 1

Como o peso está igualmente distribuído entre os dois pés, temos uma força normal para cima de módulo , atuando a do ponto , causando momento no sentido horário (negativo).

Além disso, a linha de ação da força trativa está a do ponto , causando momento no sentido anti-horário (positivo).

Assim, temos:

Passo 2

Através da equação de equilíbrio de forças na horizontal, podemos calcular a componente da força em :

Passo 3

Agora, usando a equação de equilíbrio de forças na vertical, calculamos a componente da força em :

Logo, o módulo da força de reação em deve ser:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3.42. Determine a massa de cada um dos dois cilindros se eles causam um deslocamento s = 0,5m quando suspensos pelos anéis em A e B. Observe que s = 0 quando os cilindros são removidos.

3.31. As molas no arranjo de cabos estão originalmente deformadas em 0,3m quando θ = 0 . Determine a força vertical F que deve ser aplicada, de modo que θ = 30 ° .

3.32. Determine a intensidade e a direção θ da força de equilíbrio F A B exercida ao longo da barra AB pelo aparato de tração mostrado. A massa suspensa é de 10k g . Despreze a dimensão da polia em A.

5.40. A plataforma possui um peso de 1,25k N e centro de gravidade em G 1 . Se ela deve suportar uma carga máxima de 2k N colocada no ponto G 2 , determine o menor contrapeso W que deve ser colocado e

5.30. Se a força F = 500N é aplicada ao cabo da dobradora de barras, determine as componentes horizontal e vertical da reação no pino A e a reação do rolete B sobre a barra lisa.