Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 106
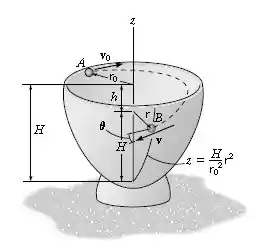
Ao pequeno rolamento de massa é dada ima velocidade em , paralela à borda horizontal de uma tigela lisa. Determine a intensidade da velocidade da bola, quando esta houver caído uma distância vertical para atingir o ponto . O ângulo é medido a partir de até a horizontal no ponto .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Primeiro precisamos analisar trigonometricamente o nosso desenho do enunciado, para nos ajudar nas continhas.
É possível notar que:
Logo:
Aplicando conservação de quantidade de movimento angular, temos:
Por conservação de energia, temos:
Resposta
Exercícios de Livros Relacionados
O conjunto parte do repouso e atinge uma velocidade angular de 150r p m sob a ação de uma força T de 20N aplicada à corda por t segundos. Determine t . Despreze o atrito e todas as massas exceto a das
A esfera de 3k g se desloca no plano x - y e tem a velocidade indicada em um determinado instante. Determine sua ( a ) quantidade de movimento linear, ( b ) quantidade de movimento angular em torno do
A única força atuando sobre um satélite da Terra que se desloca fora da atmosfera terrestre é a atração gravitacional radial. O momento desta força é nulo em torno do centro da Terra tomado como um po
A esfera de 6k g e o bloco de 4k g (mostrado em corte) estão presos ao braço de massa desprezível que gira no plano vertical em torno de um eixo horizontal em O . O tampão de 2k g é liberado a partir
A força central de atração F sobre um satélite da Terra não pode ter nenhum momento em tordo do centro O da Terra. Para a órbita elíptica específica com eixos maior e menor conforme indicado, um satél